Exercises

Precalculus for Everybody

Chapter 3 The Conics

The Parabola

In the exercises, from 1 to 5, find the focus, the directrix and \(\boldsymbol{L}\), the length of the latus rectum (focal diameter) of the parabola.

  1. \[ x^2=4y \]
  2. \[ 3x^2 + 4y= 0 \]
  3. \[ y^2 - 6x = 0 \]
  4. \[ y^2 + 20x = 0 \]
  5. \[ 4y^2 + x = 0 \]

In the exercises, from 6 to 10, find the vertex, the axis, the focus, the directrix and \(\boldsymbol{L}\), the length of the latus rectum (focal diameter) of the parabola.

  1. \[ x^2-4x-8y=-12 \]
  2. \[ y^2+10y=x-26 \]
  3. \[ y^2-4y=2x+4 \]
  4. \[ 4x^2+4x+4y+1=0 \]
  5. \[ 9x^2+24x+72y+88=0 \]

In the exercises, from 11 to 23, find a equation of the parabola with the given properties

  1. Focus \((-6, 0)\), directrix: \(x = 6\)
  2. Focus \((0, 4)\), directrix: \(y = -4\)
  3. Focus \((2, 5)\), directrix: \(y=-1\)
  4. Focus \(\left( -\frac{7}{8}, -2 \right)\), directrix: \(x = - \frac{9}{8}\)
  5. Vertex \((-2, 2)\), directrix: \(x = 2\)
  6. Vertex \((-2, 2)\), directrix: \(y=-2\)
  7. Vertex \((3, 1)\), focus: \((3, 5)\)
  8. Vertex \((0, 0)\), axis: \(x = 0\), passes through \((3, -2)\)
  9. Vertex (1, 2), axis: paralel to X-axis, passes through (5, 8)
  10. Vertex \((1,-2)\), axis: paralel to Y-axis, latus rectum: 6
  11. Directrix: \(x=-2\), axis: \(y=1\), latus rectum: 8
  12. Endpoints of the latus rectum: \((1, 1)\)   and   \((7, 1)\). It opens upwards.
  13. Vertex \((0, 0)\), endpoints of latus rectum: \((-4, \, k)\)   and   \((4, \, k)\). It opens downwards.

  14. A ball is thrown horizontally from the edge of the rooftop of a 64 meter high building.

    The trajectory of the ball is a parabola with its vertex at the edge of the roof, having an axis coincident with the wall adjacent to this edge. The ball passes through a point that is 20 meters away from the wall when its height is 16 meters.

    1. Find a equation of the ball trajectory using the coordinate system, where the origin lies on the vertex and the Y-axis coincides with the axis of the parabola.
    2. Find the distance to the wall from the point where the ball hits the floor.
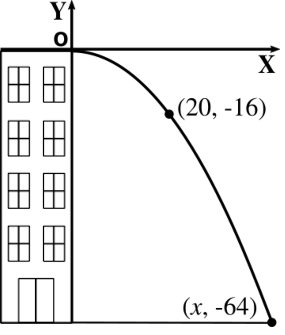
    ball thrown from the rooftop of a building
    1. Find a equation of the ball trajectory using the coordinate system, where the origin lies on the vertex and the Y-axis coincides with the axis of the parabola.
    2. Find the distance to the wall from the point where the ball hits the floor.
  15. A lighthouse has a parabolic mirror of 2\(cm\). of a depth, and a rim with a diameter of 12\(cm\). At what distance from the vertex is placed the light source if the reflected rays are parallel to the axis of the parabola?
  16. A dish of a parabolic antenna has a rim of 1\(m\). of diameter, and the receptor lies on its center. Find the depth of the dish.
  17. The towers of a suspension bridge are 150\(m\). apart, and rise 23\(m\). above the road. The cable between the towers has the shape of a parabola, of which the lowest point is 8\(m\). above the road.
    1. Find an equation of the parabola determined by the cable.
    2. Find the height of the cable at 15\(m\). from the tower.

  18. A bridge is held over a concrete parabolic arch.

    This arch has a length of 200 feet at water level, and a height of 50 feet at its center.

    1. Find an equation of the parabola using the coordinate system given in the figure.
    2. Find the height at water level of the arc at 70 feet from its right end.
    parabolic arched bridge
    1. Find an equation of the parabola using the coordinate system given in the figure.
    2. Find the height at water level of the arc at 70 feet from its right end.
  19. A comet has a parabolic orbit with the sun on its focus. When the comet is at a distance of 60 millions of \(Km\). away from the sun, the line passing through the sun and the comet forms a \(60^{\circ}\) angle with the axis of the parabola. Find shortest distance between the comet and the sun.

  20. A satellite was placed in parabolic orbit with focus at the center of the moon.

    When the satellite is 5,814 \(km\). away from the lunar surface, the axis of the parabola, and the straight line passing through the satellite and the center of the moon, form an angle of \(60^{\circ}\). The shortest distance between the satellite and the lunar surface is 150 \(km\).

    Find the radio of the moon.

    Hint: \(p = 150 + r\) and solved problem 3.2.5.

    parabola with focus located at the center of the moon

    Find the radio of the moon.

    Hint: \(p = 150 + r\) and solved problem 3.2.5.

  21. Find the standard form of the equation of a parabola whose axis is parallel to the X-axis, passing through the points (3, 1), (4, 3) and (12, 7).

    Hint: The three points satisfy the equation \((y- h)^2 = 4p(x- k)\).

  22. Find the standard form of the equation of a parabola whose axis is parallel to the Y-axis, passing through the points (1,0), (-1,6) and (2,3).
  23. Prove that the equation of the tangent line to the parabola \(y^2 = 4px\) at any point \(P=(x_1, y_1)\) is \(y_1y = 2p(x + x_1)\).

    Hint: See the solved problem 3.2.6.

  1. \[ F = (0, \, 1), \; y = -1, \; L = 4 \]
  2. \[ F = \left( 0, \, -\frac{1}{3} \right), \; y = \frac{1}{3}, \; L = \frac{4}{3} \]
  3. \[ F = \left( \frac{3}{2}, \, 0 \right), \; x = -\frac{3}{2}, \; L = 6 \]
  4. \[ F = (-5, \, 0), \; x = 5, \; L = 20 \]

  5. \(F = \left( -\frac{1}{16}, \, 0 \right)\),   \(x = \frac{1}{16}\),   \( L = \frac{1}{4}\)

  6. \(V=\left( 1, \, \frac{11}{8} \right)\),   \(x = 1\),   \(F = \left( 1, \, \frac{27}{8} \right)\),   \(y = -\frac{5}{8}\),   \(L = 8\)

  7. \(V = (1, \, -5)\),   \(y = -5\),   \(F = \left( \frac{5}{4}, \, -5 \right)\),   \(x = \frac{3}{4}\),   \(L = 1\)

  8. \(V = (-4, \, 2)\),   \(y = 2\),   \(F = \left( -\frac{7}{2}, \, 2 \right)\),   \(x = -\frac{9}{2}\),   \(L = 2\)

  9. \(V = \left( -\frac{1}{2}, \, 0 \right)\),   \(x = -\frac{1}{2}\),   \(F = \left( -\frac{1}{2}, \, -\frac{1}{4} \right)\),   \(y = \frac{1}{4}\),   \(L = 1\)

  10. \(V = \left( -\frac{4}{3}, \, -1 \right)\),   \(x = -\frac{4}{3}\),   \(F = \left( -\frac{4}{3}, \, -3 \right)\),   \(y = 1\),   \(L = 8\)

  11. \[ y^2 = – 24x \]
  12. \[ x^2 = 16 y \]
  13. \[ (x – 2)^2 = 12 (y – 2) \]
  14. \[ 2 (y + 2)^2 = x + 1 \]
  15. \[ (y – 2)^2 = – 16 (x + 2) \]
  16. \[ (x + 2)^2 = 16 (y – 2) \]
  17. \[ (x – 3)^2 = 16 (y – 1) \]
  18. \[ 2 x^2 = – 9y \]
  19. \[ (y – 2)^2 = 9(x – 1) \]

  20. \((x – 1)^2 = 6 (y + 2)\)   or   \((x – 1)^2 = – 6 (y + 2)\)

  21. \((y – 1)^2 = 8x\)   or   \((y – 1)^2 = – 8(x + 4)\)

  22. \[ (x – 4)^2 = 6 \left( y + \frac{1}{2} \right) \]
  23. \[ x^2 = -8y \]
  24.  

    1. \(x^2 = -25y\)

    2. \(40 \, m.\)

  25. \[ 4.5 \; cm. \]
  26. \[ 25 \; cm \]
  27.  

    1. \(x^2 = 375 (y – 8)\)

    2. \(17.6 \; m.\)

  28.  

    1. \(x^2 = -200(y – 50)\)

    2. \(45.5\) feet

  29. 15 million \(Km\)

  30. \(r = 1,303.5 \, km\)

  31. \[ (y – 1)^2 = 4 (x – 3) \]
  32. \[ \left( x – \frac{3}{4} \right)^2 = \frac{1}{2} \left( y – \frac{1}{8} \right) \]