Exercises

Precalculus for Everybody

Chapter 4. Real Functions

Real Functions and their Graphs

  1. If \(f(x)=\frac{x}{x+1}\), find:

    1. \[ f(3) \]
    2. \[ f \left( 1+\sqrt{x} \right) \]
    3. \[ f(2+h) - f(2) \]
    4. \[ f(a+h) - f(a) \]

  2. if \( g(x) = x + \frac{(x-2)^2}{4} \) find:

    1. \[ g(2) \]
    2. \[ g(a+2) \]
    3. \[ g(a+h)-g(a) \]

In the exercises, from 3 to 8, find the domain and the range of the given function:

  1. \[ f(x) = \sqrt{x-9} \]
  2. \[ g(x) = \frac{ \sqrt{16-x^2} }{3} \]
  3. \[ h(x) = \frac{ \sqrt{x^2-4} }{2} \]
  4. \[ u(x) = \sqrt[3]{x-2} \]
  5. \[ f(x) = \frac{x^2-4}{x} \]
  6. \[ y = \sqrt{ x(x-2) } \]

In the exercises, from 9 to 14, find the domain of the function

  1. \[ g(x) = \frac{6}{ \sqrt{9-x} -2 } \]
  2. \[ y = \frac{1}{ \sqrt{x^2-4}-2 } \]
  3. \[ y = \sqrt{ 4 - \frac{1}{x} } \]
  4. \[ y = \frac{1}{4-\sqrt{1-x}} \]
  5. \[ y = \sqrt{ \frac{x+1}{2-x} } \]
  6. \[ y = \sqrt[4]{ \frac{x+5}{x-3} } \]

In the exercises, from 15 to 16, find the domain, range and graph the function.

  1. \[ g(x) = \begin{cases} \left| x \right|, \; \text{ si } \; \left| x \right| \leq 1 \\[.5em] \hspace{0.9em} 1, \; \text{ si } \; \left| x \right| > 1 \end{cases} \]
  2. \[ f(x) = \begin{cases} \hspace{1em} \sqrt{-x}, \; \text{ si } \; x < 0 \\[.5em] \hspace{2.5em} x, \; \text{ si } \; 0 \leq x \leq 2 \\[.5em] \sqrt{x-2}, \; \text{ si } \; x > 2 \end{cases} \]

  3. Prove that:

    1. If the graph of \(f\) is symmetric respect to the Y-axis, then \(f\) is even.
    2. If the graph of \(f\) is symmetric respect to the origin, then \(f\) is odd.
  4. If \(f(x+1) = (x-3)^2\) find \(f(x-1)\).

  5. Find the quadratic function:

    \[ f(x)= ax^2 + bx \quad \text{such that} \quad f(x)-f(x-1)=x,\; \forall x \in \mathbb{R} \]
    \[ \begin{aligned} &f(x)= ax^2 + bx \quad \text{such that} \\[1em] &f(x)-f(x-1)=x,\; \forall x \in \mathbb{R} \end{aligned} \]
  6. A hotel has 40 rooms. The manager knows that when the price of a room is 30 dollars, all the rooms get rented. However, for every 5 dollars he increases the rent, a room goes unoccupied. If the maintenance cost of an occupied room is 4 dollars, express the profit of the hotel as a function of the number \(x\) of occupied rooms.
  7. When the daily production of certain article does not exceed 1,000 units, the profit is 4,000 dollars per unit. If the number of articles produced exceed 1,000, the profit decreases by 10 dollars for each article exceeding 1,000 units. Express the daily profit as a function of the number \(x\) of produced articles.
  8. A farm is planting orange trees. If 80 trees per hectare are planted, each plant produces an average of 960 oranges. For each additional plant sown, the production drops by an average of 10 oranges per plant. Express the production \(p(x)\) of oranges per hectare as a function of the number \(x\) of orange trees per hectare.
  9. For sending a box by mail, the administration requires that the base must be a square, for which the sum of its dimensions (length + width + height) cannot exceed 150 $cm$. Express the volume of the box with the maximum sum of its dimensions as a function of the length \(x\) of the base side.

  10. A wire of 12\(m\). of length is cut into two pieces.

    One of them is used to build a circle, and the other, to build a square. Con uno de ellos se forma una circunferencia y con el otro un cuadrado.

    Express the area enclosed by the two figures as a function of the radium \(r\).of the circle.

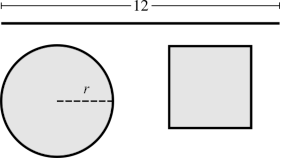
    wires with the shape of a circle and a square
    wires with the shape of a circle and a square

    Express the area enclosed by the two figures as a function of the radium \(r\).of the circle.

  11. The perimeter of an isosceles triangle is 36\(cm\). Express the area of the triangle as a function of the length \(x\) of one of the two equal sides.

  12. A window has the form of a rectangle crowned by a semicircle.

    The window has a perimeter of 7\(m\).

    Express the area of the window as a function of the width \(x\) of the rectangle.

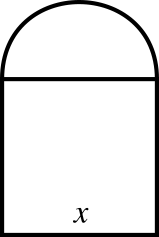
    Window with the shape of a square crowned by a semicircle

    Express the area of the window as a function of the width \(x\) of the rectangle.

  13. A factory requires to build boxes with an open top.

    Metal sheets of 80\(cm\) by 50\(cm\) will be implemented as raw material.

    Equal squares will be cut out at each corner. Then, the sides will be folded upward, as shown in the figure.

    If \(x\) is the length of the side of the small square, express the volume of the box as a function of \(x\).

    open box
    open box

    If \(x\) is the length of the side of the small square, express the volume of the box as a function of \(x\).

  14. A book will be published. Each page must have 3\(cm\). of top and button margins, and 2\(cm\). of lateral margins.

    The written area of the pages must be 252\(cm^2\).

    Express the area as a function of the width \(x\) of the written part of each page.

    página de un libro márgenes

    Express the area as a function of the width \(x\) of the written part of the page.

  1.  
    1. \[ \frac{3}{4} \]
    2. \[ \frac{1 + \sqrt{2}}{2 + \sqrt{2}} \]
    3. \[ \frac{h}{3(h + 3)} \]
    4. \[ \frac{h}{(a + 1) (a + h + 1)} \]
  2.  
    1. \[ 2 \]
    2. \[ \frac{1}{4} a^2 + a + 2 \]
    3. \[ \frac{h^2 + 2ah}{4} \]

  3. Dom\((f) = [ 9, \, +\infty)\),   Rang\((f) = [0, \, +\infty)\)

  4. Dom\((g) = [-4, \, 4]\),   Rang\((g) = \left[ 0, \, \frac{4}{3} \right]\)

  5. Dom\((h) = (-\infty, \, 2] \cup [2, \, +\infty)\),   Rang\((h) = [0, \, +\infty)\)

  6. Dom\((u) =\) Rang\((u) = \mathbb{R}\)

  7. Dom\((f) = \mathbb{R} – \{ 0 \}\),   Rang\((f) = \mathbb{R}\)

  8. Dom\((y) = (-\infty, \, 0] \cup [2, \, +\infty)\),   Rang\((y) = [0, \, +\infty)\)

  9. Dom\((g)= (-\infty, \, 9] – \{ 5 \}\)

  10. Dom\((y) = (-\infty, \, -2] \cup [2, \, +\infty) – \{ -2 \sqrt{2}, \, 2 \sqrt{2}\}\)
    \[ \begin{aligned} &\text{Dom}(y) = (-\infty, \, -2] \\[.5em] &\hspace{2em} \cup [2, \, +\infty) – \{ -2 \sqrt{2}, \, 2 \sqrt{2}\} \end{aligned} \]

  11. Dom\((y) = (- \infty, \, 0 ) \cup \left[ \frac{1}{4}, \, +\infty \right)\)

  12. Dom\((y) = (-\infty, \, 1] – \{ -15 \}\)

  13. Dom\((y) = [-1, \, 2)\)

  14. Dom\((y) = (-\infty, \, 5] \cup (3, \, + \infty)\)

  15. Dom\((y) = \mathbb{R}\),   Rang\((y) = [0, \, 1]\)
  16. \(\text{Dom}(y) = \mathbb{R}, \, \text{Rang}(y) = [0, \, +\infty)\)
  1. \[ f(x – 1) = (x – 5)^2 \]
  2. \[ f(x) = \frac{1}{2} x^2 + \frac{1}{2}x \]
  3. \[ U(x) = 226x – 5x^2 \]
  4. \[ G(x) = \begin{cases} 4,000 x, \hspace{3em} \text{si } \; 0 \leq x \leq 1,000 \\ 4,000,000 + (x – 1,000)(14,000 – 10x), \; \text{ si } x > 1,000 \end{cases} \]
    \[ \begin{aligned} G(x) = \begin{cases} 4,000 x, \\ \hspace{2em} \text{si } \; 0 \leq x \leq 1,000 \\[1em] 4,000,000 \\ \hspace{1em}+ \; (x – 1,000) \\ \hspace{2em} \times(14,000 – 10x), \\ \hspace{4em} \text{si } x > 1,000 \end{cases} \end{aligned} \]
  5. \[ P(x) = 1,760 x – 10x^2 \]
  6. \[ V(x) = x^2 (150 – 2x) \]
  7. \[ A(r) = \pi r^2 + \frac{1}{4}(6 – \pi r)^2 \]
  8. \[ A(x) = 6 (18 – x) \sqrt{x – 9} \]
  9. \[ A(x) = \frac{x}{8}(28 – 4x – \pi x) \]
  10. \[ V(x) = 4x (40 – x) (25 – x) \]
  11. \[ A(x) = \frac{1}{x}(x + 4)(252 + 6x) \]