Exercises

Precalculus for Everybody

Chapter 4. Real Functions

New Functions from Old Functions

  1. Sketch the following graphs using the graph of \(f(x)=x^3\):

    1. \[ y = x^3 - 3 \]
    2. \[ y = (x -1)^3 \]
    3. \[ y = -x^3 + 1 \]
    4. \[ y = -(x-1)^3 + 1 \]

  2. Sketch the following graphs using the graph of \(f(x)=\cfrac{1}{x}\):

    1. \[ y = \frac{1}{x} -2 \]
    2. \[ y = \frac{1}{x-2} \]
    3. \[ y = - \frac{1}{x} \]
    4. \[ y = \frac{1}{x-2} +5 \]

  3. Sketch the following graphs using the graph of \( y = \lfloor x \rfloor \):

    1. \[ y = - \lfloor x \rfloor \]
    2. \[ y = \lfloor 2x \rfloor \]
    3. \[ y = \frac{1}{2} \lfloor x \rfloor \]

  4. Using the translation and reflection techniques, and the graph of \(y=\sin x\), graph the function \(y=1- \sin(x - \frac{\pi}{2})\).

  5. Considering the graph of \(y= \cos x\):

    1. sketch the graph of \(y = -3\cos 4x\) using transformation techniques.

    2. find the period of \(y = -3\cos 4x\).

In the exercises, from 6 to 8, find \(\boldsymbol{f+g,\; f-g,\; fg}\) and \(\boldsymbol{f/g}\), with their respective domains.

  1. \[ f(x) = \cfrac{1}{1-x},\quad g(x) = \sqrt{2-x} \]
  2. \[ f(x) = \sqrt{16-x^2},\quad g(x) = \sqrt{x^2-4} \]
    \[ \begin{aligned} &f(x) = \sqrt{16-x^2}, \\[1em] &g(x) = \sqrt{x^2-4} \end{aligned} \]
  3. \[ f(x) = \cfrac{1}{\sqrt{4-x^2}},\quad g(x) = \sqrt[3]{x} \]

In the exercises, from 9 to 11, find the domain of the function.

  1. \[ f(x) = \sqrt{4-x} + \sqrt{x-4} \]
  2. \[ f(x) = \sqrt{-x} + \cfrac{1}{\sqrt{x+2}} \]
  3. \[ g(x) = \cfrac{ \sqrt{3-x} + \sqrt{x+2} }{ x^2-9 } \]

In the exercises, from 12 to 16, find \(\boldsymbol{f \circ g,\,g \circ f,\,f \circ f}\)   and   \(\boldsymbol{g \circ g}\), with their respective domains.

  1. \[ f(x) = x^2-1,\; g(x) = \sqrt{x} \]
  2. \[ f(x) = x^2,\; g(x) = \sqrt{x-4} \]
  3. \[ f(x) = x^2-x,\; g(x) = \cfrac{1}{x} \]
  4. \[ f(x) = \cfrac{1}{1-x},\; g(x) = \sqrt[3]{x} \]
  5. \[ f(x) = \sqrt{x^2-1},\; g(x) = \sqrt{1-x} \]

In the exercises, from 17 to 18, find \(\boldsymbol{f \circ g \circ h}\).

  1. \(f(x) = \sqrt{x}\),   \(g(x) = \cfrac{1}{x}\),   \(h(x) = x^2-1\)

  2. \(f(x) = \sqrt[3]{x}\),   \(g(x) = \cfrac{x}{1+x}\),   \(h(x) = x^2-x\)

  3. If \(f(x)=\cfrac{1}{1-x}\), find \(f \circ f \circ f\) with its domain.

In the exercises, from 20 to 23, find two functions \(\boldsymbol{f}\) and \(\boldsymbol{g}\) such that \(\boldsymbol{F=f \circ g}\)}.

  1. \[ F(x) = \cfrac{1}{1+x} \]
  2. \[ F(x) = -3 + \sqrt{x} \]
  3. \[ F(x) = \sqrt[3]{ (2x-1)^2 } \]
  4. \[ F(x) = \cfrac{1}{ \sqrt{ x^2 - x + 1 } } \]

In the exercises, from 24 to 26, find \(\boldsymbol{f,\, g}\)   and   \(\boldsymbol{h}\) such that:

\[ \boldsymbol{ F= f \circ g \circ h } \]
  1. \[ F(x) = \frac{x^2}{1+x^2} \]
  2. \[ F(x) = \sqrt[3]{ x^2 + \mid x \mid + 1 } \]
  3. \[ F(x) = \sqrt[4]{ \sqrt{x} - 1 } \]
  4. If \(f(x)=2x+3\) and \(h(x)=2x^2-4x+5\) find a function \(g\) such that \(f \circ g=h\).
  5. If \(f(x)=x-3\) and \(h(x)=\cfrac{1}{x-2}\) find a function \(g\) such that \(g \circ f= h\).
  1.  

    1. \(y = x^3 – 3\)

    2. \(y = (x – 1)^3\)

    3. \(y = -x^3 + 1\)

    4. \(-y = (x – 1)^3 + 1\)

  2.  

    1. \(y = \cfrac{1}{x} – 2\)

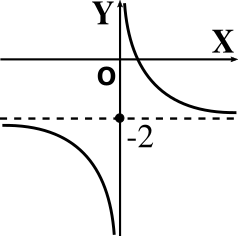
    2. \(y = \cfrac{1}{x-2}\)

    3. \(y = – \cfrac{1}{x}\)

    4. \(y = \cfrac{1}{x – 2} + 5\)

  3.  

    1. \(y = – \lfloor x \rfloor\)

    2. \(y = \lfloor 2x \rfloor\)

    3. \(y = \cfrac{1}{2} \lfloor x \rfloor \)

  4.  
    1.  
  5.  
    1.  

    2. periodo \(= \cfrac{2 \pi}{4} = \cfrac{\pi}{2}\)

  6. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = (-\infty, \, 1) \cup (1, \, 2]\),

    \(\text{Dom}\left( \frac{f}{g} \right) = ( – \infty, \, 1 ) \cup (1, \, 2 )\)

  7. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = [-4, \, -2] \cup [2, \, 4],\)

    \(\text{Dom}\left( \frac{f}{g} \right) = [-4, \, -2)\) \(\cup (2, \, 4]\)

  8. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = (-2, \, 2)\),

    \(\text{Dom}\left( \frac{f}{g} \right) = (-2, \, 2) – \{ 0 \}\)

  9. \(\text{Dom}(f) = 4\)

  10. \(\text{Dom}(f) = (-2, \, 0]\)

  11. \(\text{Dom}(g) = [-2, \, 3 )\)

  12. \((f \circ g)(x) = x – 1\),   \(\text{Dom}(f \circ g) = [0, \, +\infty)\)

    \((g \circ f)(x) = \sqrt{ x^2 – 1 }\),   \(\text{Dom}(g \circ f) = (-\infty, \, -1] \cup [1, \, +\infty)\)

    \((f \circ f)(x) = x^4 – 2x^2\),   \(\text{Dom}(f \circ f) = \mathbb{R}\)

    \((g \circ g)(x) = \sqrt[4]{x}\),   \(\text{Dom}(g \circ g) = [0, \, +\infty)\)

  13. \((f \circ g)(x) = x – 4\),   \(\text{Dom}(f \circ g) = [4, \, +\infty)\),

    \((g \circ f)(x) = \sqrt{ x^2 – 4 }\),   \(\text{Dom}(g \circ f) = (-\infty, \, -2] \cup [2, \, +\infty)\)

    \((f \circ f)(x) = x^4\),   \(\text{Dom}(f \circ f) = \mathbb{R}\)

    \((g \circ g)(x) = \sqrt{ \sqrt{x – 4} – 4 }\),   \(\text{Dom}(g \circ g) = [20, \, +\infty)\)

  14. \((f \circ g)(x) = \cfrac{1}{x^2} – \cfrac{1}{x}\),   \(\text{Dom}(f \circ g) = \mathbb{R}- \{ 0 \}\)

    \((g \circ f)(x) = \cfrac{1}{x^2 – x}\),   \(\text{Dom}(g \circ f) = \mathbb{R} – \{ 0, \, 1 \}\)

    \((f \circ f)(x) = x^4 – 2x^3 + x\),   \(\text{Dom}(f \circ f) = \mathbb{R}\)

    \((g \circ g)(x) = x\),   \(\text{Dom}(g \circ g) = \mathbb{R} – \{ 0 \}\)

  15. \((f \circ g)(x) = \cfrac{ 1 }{1 – \sqrt[3]{x}}\),   \(\text{Dom}(f \circ g) = \mathbb{R} – \{ 1 \}\)

    \((g \circ f)(x) = \cfrac{1}{\sqrt[3]{ 1 – x }}\),   \(\text{Dom}(g \circ f) = \mathbb{R} – \{ 1 \}\)

    \((f \circ f)(x) = \cfrac{x – 1}{x}\),   \(\text{Dom}(f \circ f) = \mathbb{R} – \{ 0, \, 1\}\)

    \((g \circ g)(x) = \sqrt[9]{x}\),   \(\text{Dom}(g \circ g) = \mathbb{R}\)

  16. \((f \circ g)(x) = \sqrt{-x}\),   \(\text{Dom}(f \circ g) =(-\infty, \, 0]\)

    \((g \circ f)(x) = \sqrt{ 1 – \sqrt{ x^2 – 1 } }\),   \(\text{Dom}(g \circ f) = \left[ -\sqrt{2}, \, -1 \right]\) \(\cup \left[ 1, \, \sqrt{2} \right] \)

    \((f \circ f)(x) = \sqrt{x^2 – 2}\),   \(\text{Dom}(f \circ f) = \left( -\infty, \, -\sqrt{2} \right]\) \(\cup \left[ \sqrt{2}, \, +\infty \right)\)

    \((g \circ g)(x) = \sqrt{ 1 – \sqrt{ 1 – x } }\),   \(\text{Dom}(g \circ g) = [0, \, 1]\)

  17. \[ (f \circ g \circ h)(x) = \sqrt{ \frac{1}{x^2 – 1} } \]
  18. \[ (f \circ g \circ h)(x) = \sqrt[3]{ \frac{x^2 – x}{ x^2 – x + 1 } } \]

  19. \((f \circ f \circ f)(x) = x, \)   \(\text{Dom}(f \circ f \circ f) = \mathbb{R}- \{ 0, \, 1 \}\)

  20. \[ f(x) = \frac{1}{x}, \, g(x) = 1 + x \]
  21. \[ f(x) = x-3, \, g(x) = \sqrt{x} \]
  22. \[ f(x) = \sqrt[3]{x}, \, g(x) = (2x – 1)^2 \]
  23. \[ f(x) = \frac{1}{x}, \, g(x) = \sqrt{ x^2 – x + 1 } \]

  24. \(f(x) = \cfrac{1}{x + 1}\),   \(g(x) = \cfrac{1}{x}\),   \(h(x) = x^2\)

  25. \(f(x) = \sqrt[3]{x}\),   \(g(x) = x + 1\),   \(h(x) = x^2 + \mid x \mid\)

  26. \(f(x) = \sqrt[4]{x}\),   \(g(x) = x – 1\),   \(h(x) = \sqrt{x}\)

  27. \[ g(x) = x^2 – 2x + 1 \]
  28. \[ g(x) = \frac{1}{x + 1} \]