Respuestas

Cálculo Diferencial para Economía y Negocios

Sección 0.2. El Sistema de los Números Reales

1. \(6\); \(\sqrt[3]{27}\); \(\sqrt{16}\)
2. \(6\); \(-11\); \(\sqrt[3]{27}\); \(0\); \(\sqrt{16}\); \(-\sqrt[3]{8}\)
3. \(\frac{2}{3}\); 6; -2,45; \(18,\overline{4}\); -11; \(\sqrt[3]{27}\);\(3+\frac{1}{2}\); \(-\cfrac{6}{5}\); 0; \(\sqrt{16}\);\(-\sqrt[3]{8}\); \(0.714285714285\ldots\)
4. \(\sqrt{3}\); \(\sqrt{2}\); \(7.151551555\ldots\); \(-\sqrt{8}\); \(\pi\)
5. Todos.
1. 2; 5
2. -6; 2; 5
3. -6; \(\frac{5}{2}\); \(-1,333\ldots\); 2; 5
4. \(\pi\)
5. Todos.
Falso, porque los números reales están formados por la unión de los números racionales y los números irracionales.
Falso, porque los elementos de \(\mathbb{\mathbb{Z}}\) son números enteros; es decir, \[ \mathbb{\mathbb{Z}}=\left\{ \ldots,-3,-2,-1,0,1,2,3,\ldots\right\}. \]
Falso, ya que, un número racional no puede tener un denominador cero.
Falso. Los enteros no negativos son \(\left\{ 0,1,2,3,\ldots\right\} \) y los naturales son \(\left\{ 1,2,3,\ldots\right\} \). El cero no es un número natural.
Verdadero. Por ejemplo, \(\frac{4}{1}=4\).
Verdadero.
Falso, porque \(\sqrt{2}=1.414213562\ldots\) la parte decimal de \(\sqrt{2}\) no termina ni se repite.
Falso, porque la parte decimal es periódica.
Verdadero.
Verdadero.
Falso, por ejemplo \(\frac{1}{2}\) es racional pero no es un entero.
Verdadero.
Verdadero, porque -2 y 7 son enteros y \(7\neq0\).
Falso, porque los números naturales son 1,2,3, y así sucesivamente.
Verdadero, porque \(5=\frac{5}{1}\).
Falso. Un número racional no puede tener al cero como denominador.
Falso, porque \(\sqrt{25}=5\), que es un entero positivo.
Verdadero.
Verdadero, porque \(\frac{7}{3}\cdot\frac{3}{7}=1\).
Falso, el inverso aditivo de 7 es -7, porque \(7+\left(-7\right)=0\).
Falso, porque \(2\left(3\cdot4\right)=2\cdot12=24\) y \(\left(2\cdot3\right)\left(2\cdot4\right)=6\cdot8=48\).
Propiedad distributiva de la multiplicación sobre la adición.
Propiedad conmutativa de la adición.
Propiedad asociativa de la multiplicación.
Propiedad conmutativa para la multiplicación.
Propiedad asociativa para la adición.
Existencia del elemento neutro de la adición.
Existencia del elemento neutro de la multiplicación.
Existencia del inverso aditivo.
Existencia del recíproco o inverso multiplicativo.
Existencia del elemento neutro de la multiplicación.
Propiedad distributiva de la multiplicación sobre la adición.
Propiedad asociativa para la adición.
2. \(\left[-7,-2\right]\) live_tv
2. \(\left(1,10\right)\) live_tv
2. \(\left(-\infty,-5\right]\cup\left[5,+\infty\right)\) live_tv
2. \(\left(-\infty,0\right)\cup\left[3,+\infty\right)\)
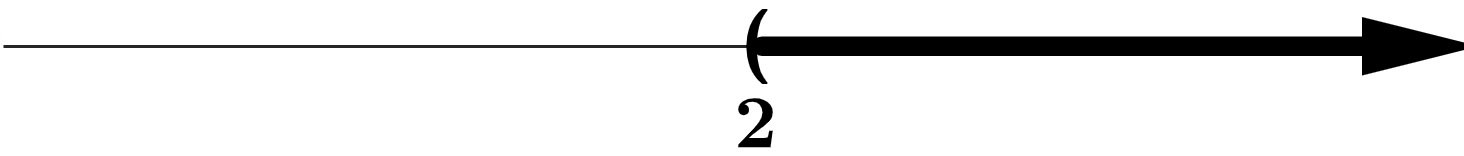
2. \(\left(2,+\infty\right)\)
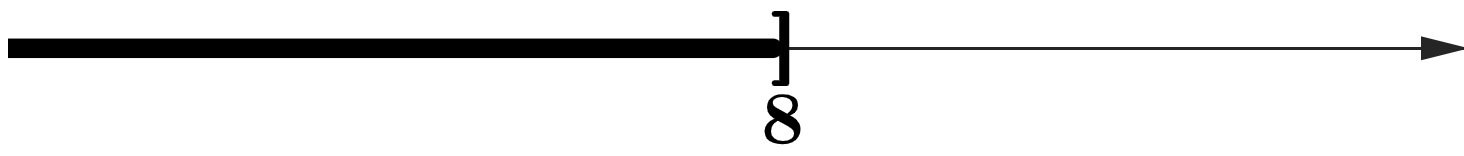
2. \(\left(-\infty,8\right]\)
\(x<0\)
\(y\geq0\)
\(q\leq\pi\)
\(2 < d < 4 \)
\(t\geq 5\)
\(-z\leq3\)
\(\frac{p}{q}\leq7\)
\(\frac{1}{w}\geq9\)
\(b>0\)
\(s\leq0\)
\(w\geq-4\)
\(\frac{1}{5} < c < \frac{1}{3}\)
\(p\leq-2\)
\(-m\geq-2\)
\(\frac{r}{s}\geq\frac{1}{5}\)
\(\frac{1}{f}\leq14\)
Verdadero.
Falso.
Verdadero.
Verdadero.
Falso.
Verdadero.
Falso.
Verdadero.
-6
-31
-867
-837
-82
\(\frac{29}{24}\)
\(-\frac{15}{28}\)
\(-\frac{19}{90}\)
\(\frac{31}{144}\)
\(-\frac{101}{420}\)
\(-\frac{109}{12}\)
\(\frac{1}{3}\)
\(-\frac{1}{90}\)
\(-\frac{1}{25}\)
\(-\frac{1}{12}\)
\(-\frac{1160}{9}\)
\(-7\)
\(\frac{19}{10}\)
\(1\)
\(-\frac{1}{5}\)
\(\frac{40}{3}\)
\(\frac{7}{80}\)
\(-\frac{2}{3}\)
\(\frac{8}{3}\)
\(-\frac{27}{290}\)
\(\frac{31}{22}\)
\(\frac{29}{11}\)