Usarémos sympy para buscar el punto medio entre dos puntos dados
from sympy import Matrix
# Definimos los puntos usando sympy.Matrix
A = Matrix([-3, 0])
B = Matrix([1, 2])
# Calculamos el punto medio
M = (A + B) / 2
# Mostramos el punto medio
M
Resultado:
\(
\begin{bmatrix}
-1 \\ 1
\end{bmatrix}
\)
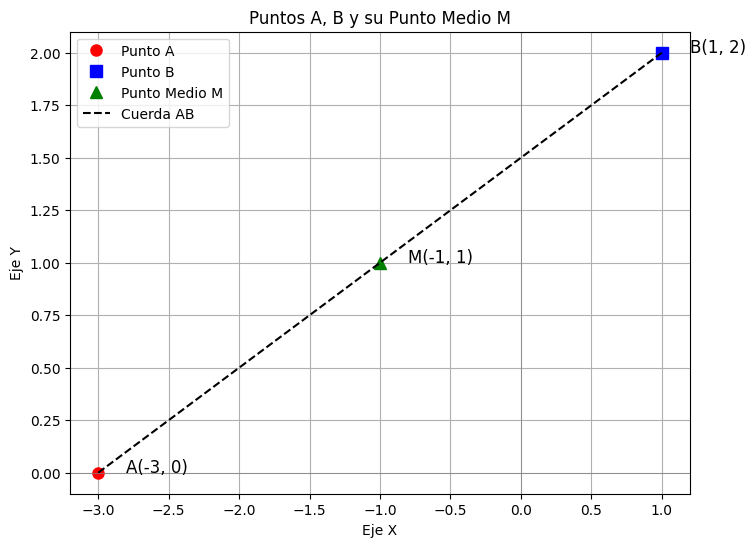
Ahora vamos a mostrar estos puntos en el plano usando la librería Matplotlib
import matplotlib.pyplot as plt
# Extraemos las coordenadas de los puntos, convitiéndolos en listas de 2 valores, ya que originalmente son matrices
A_coords = A.tolist()
B_coords = B.tolist()
M_coords = M.tolist()
# Crear la figura y los ejes
plt.figure(figsize=(8, 6))
# Graficar los puntos
plt.plot(A_coords[0][0], A_coords[1][0], 'ro', markersize=8, label='Punto A') # 'ro' para círculo rojo
plt.plot(B_coords[0][0], B_coords[1][0], 'bs', markersize=8, label='Punto B') # 'bs' para cuadrado azul
plt.plot(M_coords[0][0], M_coords[1][0], 'g^', markersize=8, label='Punto Medio M') # 'g^' para triángulo verde
# Graficar la cuerda entre A y B
plt.plot([A_coords[0][0], B_coords[0][0]], [A_coords[1][0], B_coords[1][0]], 'k--', label='Cuerda AB') # 'k--' para línea de puntos negra
# Anotar los puntos con sus etiquetas
plt.text(A_coords[0][0] + 0.2, A_coords[1][0], f'A({A_coords[0][0]}, {A_coords[1][0]})', fontsize=12)
plt.text(B_coords[0][0] + 0.2, B_coords[1][0], f'B({B_coords[0][0]}, {B_coords[1][0]})', fontsize=12)
plt.text(M_coords[0][0] + 0.2, M_coords[1][0], f'M({M_coords[0][0]}, {M_coords[1][0]})', fontsize=12)
# Configurar el gráfico
plt.title('Puntos A, B y su Punto Medio M')
plt.xlabel('Eje X')
plt.ylabel('Eje Y')
plt.grid(True)
plt.axhline(0, color='gray', linewidth=0.5) # Línea en el eje X
plt.axvline(0, color='gray', linewidth=0.5) # Línea en el eje Y
plt.legend()
plt.show()
Resultado: