Vamos a demostrar que una ecuación dada es una elipse, usando sympy.
import sympy as sym
# Definimos las variables
x, y = sym.symbols('x y')
# Definimos la ecuación
expresion = sym.Eq(9*x**2 - 16*y**2, 144)
# Mostramos la ecuación
print("Expresión original:")
expresion
Resultado:
Expresión original:
\(
9x^2 − 16y^2 = 144
\)
Ahora graficamos la ecuación usando Matplotlib y Numpy.
import numpy as np
import matplotlib.pyplot as plt
# 1. Creamos una rejilla de puntos x e y (entre -5 y 5 para cubrir la elipse)
# np.linspace genera 400 puntos distribuidos uniformemente entre los límites.
x = np.linspace(-5, 5, 400)
y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(x, y)
# 2. Definimos la ecuación. Buscamos en donde esta expresión vale 144.
Z = 9 * X**2 + 16 * Y**2
# 3. Dibujamos el contorno solo para el nivel 144
plt.contour(X, Y, Z, levels=[144], colors='blue')
# Configuración visual importante
plt.gca().set_aspect('equal') # Asegura que la escala de x e y sea la misma
plt.grid(True)
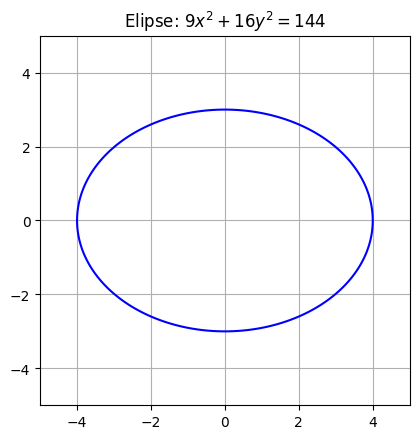
plt.title("Elipse: $9x^2 + 16y^2 = 144$")
plt.show()
Resultado: