Cal. Diferencial Sec. 4.3

Monotonía, concavidad y criterios para extremos locales

Bosquejar el gráfico de una función \(f\) que cumple:

\[ f(2) = -2, \]

\[ f'(2) = 0, \]

\[ f''(x) > 0,\, \forall x \in \mathbb{R} \]
Bosquejar el gráfico de una función \(f\) que cumple:

\[ f(2) = 2, \]

\[ \text{No existe }f'(2), \]

\[ f''(x) > 0 \; \text{ si } \; x < 2, \]

\[ f''(x) < 0 \; \text{ si } \; x > 2 \]
El dibujo adjunto es el gráfico de la derivada de una función continua \(f\).

Determinar:
1. Los números críticos de \(f\).
2. Los intervalos de monotonía.
3. Los números críticos que correspondan a máximos o mínimos locales.
1. Los números críticos de \(f\).
2. Los intervalos de monotonía.
3. Los números críticos que correspondan a máximos o mínimos locales.
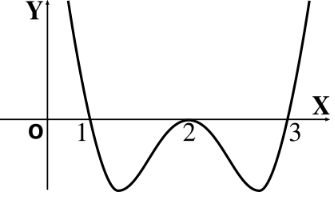
El dibujo adjunto es el gráfico de la segunda derivada de una función \(f\).

Determinar:
1. Los números críticos de segundo orden.
2. Los intervalos de concavidad.
3. Los números críticos de segundo orden que correspondan a puntos de inflexión.
1. Los números críticos de segundo orden.
2. Los intervalos de concavidad.
3. Los números críticos de segundo orden que correspondan a puntos de inflexión.

En los problemas del 5 al 18, hallar:

Los números críticos.
Intervalos de monotonía.
Los extremos locales.
Los números críticos de segundo orden.
Intervalos de concavidad.
Puntos de inflexión.

\[ f(x) = -2x^2- 8x + 3 \]
\[ f(x) = x^3 - 3x + 1 \]
\[ f(x) = x^3 + 3x^2 - 9x + 12 \]
\[ g(x) = x^4 - 2x^2 + 4 \]
\[ h(x) = x^4 + 2x^3 - 3x^2 - 4x + 1 \]
\[ g(x) = \frac{x}{x-2} \]
\[ f(x) = (x - 6)\sqrt{x} \]
\[ f(x) = 2x^{1/3} + x^{2/3} \]
\[ g(x) = x \mid x \mid \]
\[ h(x) = x - \ln x \]
\[ f(x) = x \mathrm{e}^{x^2} \]
\[ f(x) = x - 2\text{ sen } x, \; \text{en } [0,\, 2\pi] \]
\[ g(x) = \cos^2 x - 2 \text{ sen } x, \text{ en } [0,\, 2\pi] \]
\[ h(x) = 2x - \text{ sen}^{-1} x, \text{ en } [-1,\, 1] \]

En los problemas 19 y 20, bosquejar el gráfico de la función continua \(\boldsymbol{f}\) que satisface las condiciones dadas.

\[ \begin{aligned}[t] & f'(x) > 0 \text{ si } x < 0 \; \text{ ó } \; 0 < x < 3,\; f'(x) < 0 \text{ si } x > 3 \\[.5em] & f'(0) = 0, \; f(0) = 1,\; f'(3) = 0, \; f(3) = 3 \\[.5em] & f''(x) < 0 \; \text{ si } \; x < 0 \; \text{ ó } \; 2 < x < 5, \; f''(x) > 0 \text{ si } 0 < x < 2 \; \text{ ó } \; x > 5 \end{aligned} \]

\[ \begin{aligned}[t] &f'(x) > 0 \; \text{ si } \; x < 0 \; \text{ ó } \; 0 < x < 3, \\[.5em] &f'(x) < 0 \; \text{ si } \; x > 3 \\[.5em] &f'(0) = 0, \; f(0) = 1,\; f'(3) = 0, \\[.5em] &\hspace{10em}f(3) = 3 \\&f''(x) < 0 \; \text{ si } \; x < 0 \; \text{ ó } \; 2 < x < 5, \\[.5em] &f''(x) > 0 \; \text{ si } \; 0 < x < 2 \; \text{ ó } \; x > 5 \end{aligned} \]
\[ \begin{aligned}[t] & f'(x) > 0 \text{ si } x < 2, \; f'(x) < 0 \text{ si } 2 < x < 5, \; f'(x) = 1 \text{ si } x > 5 \\[.5em] & f(0) = f(4) = 0, \; f(2) = 2. \; \text{ No existen } f'(2) \; \text{ y } \; f'(5) \\[.5em] & f''(x) < 0 \text{ si } x < 0 \; \text{ ó } \; 4 < x < 5, \; f''(x) > 0 \; \text{ si } \; 0 < x < 2 \; \text{ ó } \; 2 < x < 4 \end{aligned} \]

\[ \begin{aligned}[t] &f'(x) > 0 \; \text{ si } \; x < 2, \\[.5em] &f'(x) < 0 \; \text{ si } \; 2 < x < 5, \\[.5em] &f'(x) = 1 \; \text{ si } \; x > 5 \\[.5em] & f(0) = f(4) = 0, \\[.5em] &f(2) = 2. \\[.5em] &\text{No existen } f'(2) \, \text{ y } \, f'(5) \\[.5em] &f''(x) < 0 \, \text{ si } \, x < 0 \; \text{ ó } \; 4 < x < 5, \\[.5em] &f''(x) > 0 \, \text{ si } \, 0 < x < 2 \\[.5em] &\hspace{8em}\text{ó } \; 2 < x < 4 \end{aligned} \]

En los problemas 21 y 22, se dan las gráficas de la derivada de una función continua \(\boldsymbol{f}\) . Determinar:

Los números críticos de \(\boldsymbol{f}\).
Los intervalos de monotonía de \(\boldsymbol{f}\).
Los números críticos que dan lugar a extremos locales.
Los números críticos de segundo orden de \(\boldsymbol{f}\).
Los intervalos de concavidad de \(\boldsymbol{f}\).
Números críticos de segundo orden que dan lugar a puntos de inflexión.
Esbozar el gráfico.

En los problemas 23 y 24 se tiene jarrones en los cuales se vierte agua a una razon constante. En cada caso, esbozar la gráfica de la función altura del agua como funcion del tiempo \(\boldsymbol{h=f(t)}\).

Mostrar la concavidad y los puntos de inflexión.

En los problemas del 25 al 28, hallar los extremos absolutos de la función dada en el intervalo indicado.

\[ h(x) = 4x^3 - 3x^4, \; (-\infty, \, +\infty) \]
\[ g(x) = 4 - 2(x - 1)^{\frac{2}{3}}, \text{ en } [0,\, +\infty) \]
\[ g(x) = x \ln x, \; [0,\, \mathrm{e}] \]
\[ h(x) = (x + 1) \mathrm{e}^{-x}, \; (-\infty, \, +\infty) \]
Probar que una función cúbica \(f(x) = ax^3 + bx^2 + cx + d\) tiene uno y sólo un punto de inflexión.
Si la función cúbica \(f(x) = ax^3 + bx^2 + cx + d\) tiene por raíces a \(r_1\), \(r_2\) y \(r_3\), probar que la abscisa del punto de inflexión es \(x = \frac{1}{3}(r_1 + r_2 + r_3)\).

Sugerencia: \(f(x) = a(x - r_1)(x - r_2)(x - r_3)\)
Si \(f\) y \(g\) son cóncavas hacia arriba en el intervalo \(I\), probar que \(f + g\) es cóncava hacia arriba en \(I\).
Si \(f\) es positiva y cóncava hacia arriba en un intervalo \(I\), probar que la función \(g(x) = [f(x)]^2\) es cóncava hacia arriba.
Sean \(f\) y \(g\) positivas y cóncavas hacia arriba en el intervalo \(I\), probar:
1. Si \(f\) y \(g\) son crecientes, entonces \(fg\) es cóncava hacia arriba en \(I\).
2. Si \(f\) y \(g\) son decrecientes, entonces \(fg\) es cóncava hacia arriba en \(I\).

Ver Respuestas

Respuestas

1. -1, 0, 2, 4
2. Decreciente \((- \infty, \, -1]\), \([0, \, 2]\) y \([2, \, 4]\).
  
  Creciente \([-1, \, 0]\) y \((4, \, +\infty)\)
3. Mín. local en -1 y 4.
  
  Máximo local en 0
1. 1, 2, 3
2. Cóncava hacia ariba en \((-\infty, \, 1)\) y \((3, \, +\infty)\).
  
  Cóncava hacia abajo en \((1, 2)\) y \((2, 3)\).
3. 1 y 3
1. -2
2. Creciente en \((-\infty, \, -2]\),
  
  decreciente en \([-2, \, +\infty)\)
3. \(f(-2) = 11\) es máx. local.
4. No tiene.
5. Cóncava hacia abajo en \((-\infty, \, +\infty)\).
6. No tiene.
1. -1, 1
2. Creciente en \((-\infty, \, -1]\) y \([1, \, +\infty)\),
  
  decreciente en \([-1, \, 1]\).
3. \(f(-1) = 3\) es máx. local,
  
  \(f(1) = -1\) es mín. local.
4. 0
5. Cóncava hacia abajo en \((-\infty, \, 0)\),
  
  cóncava hacia arriba en \((0, \, +\infty)\)
6. \(( 0, \, f(0) ) = (0, \, 1)\)
1. -3, 1
2. Creciente en \((-\infty, \, -3]\) y \([1, \, +\infty)\),
  
  decreciente en \((-3, \, 1]\)
3. máx. local: \(f(-3) = 39\),
  
  mín. local: \(f(1) = 7\)
4. -1
5. Cóncava hacia arriba en \((-\infty, \, -1 )\),
  
  cóncava hacia abajo en \((-1, \, +\infty)\)
6. \(\left( -1, \, f(-1) \right) = (-1, \, 23)\)
1. -1, 0, 1
2. Creciente: \([-1, \, 0]\) y \([1, \, +\infty)\),
  
  decreciente: \((-\infty, \, -1]\) y \([0, \, 1]\)
3. Mín local: \(f(-1) = 3\) y \(f(1) = 3\),
  
  máx. local: \(f(0) = 4\)
4. \(-\cfrac{\sqrt{3}}{3}, \, \cfrac{\sqrt{3}}{3}\)
5. Cóncava hacia arriba: \(\left( -\infty, \, -\frac{\sqrt{3}}{3} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, +\infty \right)\),
  
  cóncava hacia abajo: \(\left( -\frac{\sqrt{3}}{3}, \, \frac{\sqrt{3}}{3} \right)\)
6. \(\left( -\frac{\sqrt{3}}{3}, \, \frac{31}{9} \right)\) y \(\left( \frac{\sqrt{3}}{3}, \, \frac{31}{9} \right)\)
1. \(-2, \, -\frac{1}{2}, \, 1\)
2. Creciente en: \(\left[ -2, \, -\frac{1}{2} \right]\) y \([1, \, +\infty)\)
  
  decreciente en: \((-\infty, \, -2)\) y \(\left[ -\frac{1}{2}, \, 1 \right]\)
3. Mín. local: \(h(-2) = -3\) y \(h(1) = -3\)
  
  máx. local: \(h \left( -\frac{1}{2} \right) = \frac{33}{16}\)
4. \(-\frac{1}{2} – \frac{ \sqrt{3} }{2}, \; -\frac{1}{2} + \frac{\sqrt{3}}{2}\)
5. Cóncava hacia arriba en: \(\left( -\infty, \, -\frac{1}{2} – \frac{ \sqrt{3} }{2} \right)\) y \(\left( -\frac{1}{2} + \frac{ \sqrt{3} }{2}, \, +\infty \right)\),
  
  cóncava hacia abajo en: \(\left( -\frac{1}{2}, \, -\frac{\sqrt{3}}{2}, \, -\frac{1}{2} + \frac{\sqrt{3}}{2} \right)\)
6. \(\left( -\frac{1}{2} – \frac{\sqrt{3}}{2}, \, h \left( -\frac{1}{2} – \frac{ \sqrt{3} }{2} \right) \right)\) \(\approx\) \(\left( -\frac{1}{2}- \frac{ \sqrt{3} }{2}, \, -0.73 \right)\)
  
  y \(\left( -\frac{1}{2} + \frac{ \sqrt{3} }{2}, \, h \left( -\frac{1}{2} + \frac{ \sqrt{3} }{2} \right) \right)\) \(\approx\) \(\left( -\frac{1}{2} + \frac{ \sqrt{3} }{2} \right)\) \(\approx\) \(\left( -\frac{1}{2} + \frac{ \sqrt{3} }{2}, \, -0.73 \right)\)
  
  \[ \begin{aligned} &\left( -\frac{1}{2} – \frac{\sqrt{3}}{2}, \, h \left( -\frac{1}{2} – \frac{ \sqrt{3} }{2} \right) \right) \\[.5em] &\hspace{3em} \approx \left( -\frac{1}{2}- \frac{ \sqrt{3} }{2}, \, -0.73 \right) \\[.5em] &\text{y:} \\[.5em] &\left( -\frac{1}{2} + \frac{ \sqrt{3} }{2}, \, h \left( -\frac{1}{2} + \frac{ \sqrt{3} }{2} \right) \right) \\[.5em] &\hspace{3em} \approx \left( -\frac{1}{2} + \frac{ \sqrt{3} }{2} \right) \\[.5em] &\hspace{3em} \approx \left( -\frac{1}{2} + \frac{ \sqrt{3} }{2}, \, -0.73 \right) \end{aligned} \]
1. No tiene
2. Decreciente: \((-\infty, \, 2)\) y \((2, \, +\infty)\)
3. No tiene
4. No tiene
5. Cóncava h. abajo: \((-\infty, \, 2)\)
  
  cóncava h. arriba: \((2, \, +\infty)\)
6. No tiene
1. 2
2. Creciente: \([2, \, +\infty)\),
  
  decreciente: \([0, \, 2]\)
3. Mín. local: \(f(2) = -4 \sqrt{2}\)
4. No tiene
5. Cóncava h. arriba: \((0, \, +\infty)\)
6. No tiene
1. -1, 0
2. Creciente: \([-1, +\infty)\),
  
  decreciente: \((-\infty,-1]\)
3. Mín. local: \(f(-1) = -1\)
4. 0, -8
5. Cóncava h. abajo: \((-\infty, \, -8)\) y \((0, \, +\infty)\),
  
  cóncava h. arriba: \((-8, \, 0)\)
6. \((-8, \, f(-8)) = (-8, \, 0)\) y \((0, \, f(0)) = (0, \, 0)\)
1. 0
2. Creciente: \((-\infty, \, +\infty)\)
3. No tiene
4. 0
5. Cóncava h. abajo: \((-\infty, \, 0)\),
  
  cóncava h. arriba: \((0, \, +\infty)\)
6. \((0, \, 0)\)
1. 1
2. Decreciente: \((0, \, 1]\)
  
  creciente: \([1, \, +\infty)\)
3. Mín. local: \(h(1) = 1\)
4. No tiene
5. Cóncava h. arriba: \((0, \, +\infty)\)
6. No tiene
1. No tiene
2. Creciente: \((-\infty, \, +\infty)\)
3. No tiene
4. 0
5. Cóncava h. abajo: \((-\infty, \, 0)\),
  
  cóncava h. arriba: \((0, \, +\infty)\)
6. \((0, \, 0)\)
1. \(\cfrac{\pi}{3}, \, \cfrac{5\pi}{3}\)
2. Decreciente: \(\left[ 0, \, \frac{\pi}{3} \right]\) y \(\left[ \frac{ 5\pi }{3}, \, 2\pi \right]\)
  
  Creciente: \(\left[ \frac{\pi}{3}, \, \frac{5\pi}{3} \right]\)
3. Mín. local: \(f \left( \frac{\pi}{3} \right) = \frac{\pi}{3} – \sqrt{3}\) \(\approx -0.7\),
  
  máx. local: \(f \left( \frac{5 \pi}{3} \right) = \frac{5\pi}{3} + \sqrt{3}\) \(\approx 7\)
4. \(\pi\)
5. Cóncava h. arriba: \((0, \, \pi)\),
  
  cóncava h. abajo: \((\pi, \, 2\pi)\)
6. \((\pi, \, f(\pi)) = (\pi, \, \pi)\)
1. \(\cfrac{\pi}{2}, \, \cfrac{3\pi}{2}\)
2. Decreciente: \(\left[ 0, \frac{\pi}{2} \right]\) y \(\left[ \frac{3\pi}{2}, 2\pi \right]\),
  
  creciente: \(\left[ \frac{\pi}{2}, \, \frac{3\pi}{2} \right]\)
3. Mín. local: \(g \left( \frac{\pi}{2} \right) = -2\)
  
  máx. local: \(g \left( \frac{3\pi}{2} \right) = 2\)
4. \(\frac{\pi}{6}, \, \frac{5\pi}{6}, \, \frac{3\pi}{2}\)
5. Cóncava hacia abajo: \(\left( 0, \, \frac{\pi}{6} \right)\), \(\left( \frac{5\pi}{6}, \, \frac{3\pi}{2} \right)\) y \(\left( \frac{3\pi}{2}, \, 2 \pi \right)\),
  
  cóncava h. arriba: \(\left( \frac{\pi}{6}, \, \frac{5\pi}{6} \right)\)
6. \(\left( \frac{\pi}{6}, g \left( \frac{\pi}{6} \right) \right) = \left( \frac{\pi}{6}, -\frac{1}{4} \right)\) y \(\left( \frac{5\pi}{6}, \, g \left( \frac{5\pi}{6} \right) \right) = \frac{5\pi}{6} – \frac{1}{4}\)
1. \(-\cfrac{\sqrt{3}}{2}, \, \cfrac{ \sqrt{3} }{2}\)
2. Decreciente: \(\left[ -1, -\frac{\sqrt{3}}{2} \right]\) y \(\left[ \frac{\sqrt{3}}{2}, \, 1 \right]\),
  
  creciente: \(\left[ -\frac{\sqrt{3}}{2}, \frac{\sqrt{3}}{2} \right]\)
3. Mín. local: \(h \left( – \frac{ \sqrt{3} }{2} \right) = – 0.68\),
  
  máx. local: \(h \left( \frac{\sqrt{3}}{2} \right) = 0.68\)
4. 0
5. Cóncava h. arriba: \((-1, \,0)\),
  
  cóncava h. abajo: \((0, \, 1)\)
6. \((0, \, 0)\)
1. 0 y 4
2. Decreciente: \((-\infty,0]\) y \([0,4]\)
  
  creciente: \([4, \, +\infty)\)
3. Mín. local en 4
4. 0 y 3
5. Cóncava h. arriba: \((-\infty, \, 0)\) y \((3, \, +\infty)\)
  
  cóncava h. abajo: \((0, \, 3)\)
6. 0 y 3
1. -2, 0, 1 y 3
2. Decreciente: \((-\infty, \, -2]\), \([-2, \, 0]\), \([1, \, 3]\),
  
  creciente: \([0, \, 1]\), \([3, \, +\infty)\)
3. Min. local en 0 y 3,
  
  máx. local en 1
4. -2 y 2
5. Cóncava h. arriba: \((-\infty,-2)\) y \((2,+\infty)\),
  
  cóncava h. abajo: \((-2, 0)\), \((0, 2)\)
6. -2 y 2
Máx. \(f(1) = 1\). Mín. no tiene
Máx. \(f(1) = 4\). Mín. no tiene
Máx. \(f(\mathrm{e}) = \mathrm{e}\). Mín. \(f\left( \frac{1}{ \mathrm{e} } \right)\) \(=\) \(- \frac{1}{ \mathrm{e} }\)
Máx. \(f(0) = 1\). Min. no tiene