Calcular la distancia entre los puntos usando sympy
Primero, definiremos los puntos usando Matrix de Sympy para calcular la distancia euclidiana entre cada par de puntos usando la función norm.
from sympy import Matrix
import math
# Definimos los puntos usando sympy.Matrix
A = Matrix([1, 1])
B = Matrix([3, 0])
C = Matrix([4, 7])
# Calcular las distancias usando el método norm()
distancia_ab = (A - B).norm()
distancia_bc = (B - C).norm()
distancia_ca = (C - A).norm()
# Mostramos la distancia entre "a" y "b"
distancia_ab
Resultado:
\(
\sqrt{5}
\)
# Mostramos la distancia entre "b" y "c"
distancia_bc
Resultado:
\(
5\sqrt{2}
\)
# Mostramos la distancia entre "a" y "c"
distancia_ca
Resultado:
\(
3 \sqrt{5}
\)
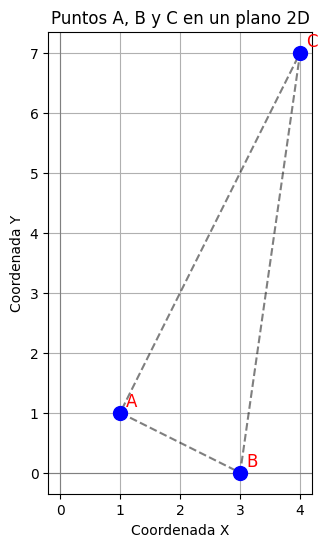
Visualizar los puntos en un gráfico
Ahora, graficaremos los puntos A, B y C para ver su distribución. Sympy puede generar graficas sencillas, pero usaremos la librería
matplotlib en esta oportunidad. No te asustes con la cantidad de parámetros, ya que estos nos permiten ajustar la gráfica a nuestro gusto o preferencia.
import matplotlib.pyplot as plt
# Extraer coordenadas para el gráfico desde los objetos Matrix de sympy
points_dict = {'A': A, 'B': B, 'C': C}
x_coords = [p[0] for p in points_dict.values()]
y_coords = [p[1] for p in points_dict.values()]
plt.figure(figsize=(8, 6))
plt.scatter(x_coords, y_coords, color='blue', s=100, zorder=5)
# s es el tamaño del marcador, zorder asegura que los puntos estén en la parte superior
# Anotar cada punto con su nombre
for label, point in points_dict.items():
plt.annotate(label, (float(point[0]) + 0.1, float(point[1]) + 0.1), fontsize=12, color='red')
# Conectar los puntos para formar un triángulo (opcional, para visualización)
plt.plot([float(A[0]), float(B[0]), float(C[0]), float(A[0])], [float(A[1]), float(B[1]), float(C[1]), float(A[1])], 'k--', alpha=0.5)
plt.title('Puntos A, B y C en un plano 2D')
plt.xlabel('Coordenada X')
plt.ylabel('Coordenada Y')
plt.grid(True)
plt.axhline(0, color='grey', linewidth=0.8) # Eje X
plt.axvline(0, color='grey', linewidth=0.8) # Eje Y
plt.gca().set_aspect('equal', adjustable='box') # Asegura que los ejes tengan la misma escala
plt.show()
Resultado: