Usaremos Sympy para encontrar la pendiente de una recta y sus intersecciones con los ejes
import sympy
import matplotlib.pyplot as plt
import numpy as np
# Definimos las variables
x, y = sympy.symbols('x y')
# Definimos la ecuación de la recta
ecuacion = sympy.Eq(2*x - 3*y + 12, 0)
print(f"Ecuación Original:")
ecuacion
Resultado:
Ecuación Original:
\(
2x−3y+12=0
\)
Hallamos la pendiente y la intersección con el eje Y
Para hallar la pendiente y la intersección con el eje Y necesitamos expresar la ecuacuón con la forma "y = mx + b", donde "m" es la pendiente, y "b" es la intersección con el eje Y.
# Resolvemos la ecuación en función de "y"
y_solved = sympy.solve(ecuacion, y)[0]
#print(f"Ecuación resuelta para 'y': y = {y_solved}")
print(f"Ecuación resuelta para 'y':")
display(y_solved)
Resultado:
Ecuación resuelta para ‘y’:
\(
\frac{2x}{3} + 4
\)
# La pendiente "m" es el coeficiente de "x". Usarémos la función coeff():
slope = y_solved.coeff(x)
print(f"Pendiente(m):")
display(slope)
Resultado:
Pendiente(m):
\(
\frac{2}{3}
\)
# La intersección con el eje Y (b) es la constante cuando x = 0
y_intercept = y_solved.subs(x, 0) #aquí sustituímos a "x" por "0" en la ecuación
print(f"Intersección con el eje Y(b):")
display(y_intercept)
Resultado:
Intersección con el eje Y(b):
\(
4
\)
Buscamos la intersección con el eje X
Para encontrar esta intersección debemos establecer que "y = 0" en la ecuación original, y luego, resolver en función de «x".
# Sustituímos y = 0 en la ecuación original y resolvemos para "x"
x_intercept_equacion = ecuacion.subs(y, 0)
x_intercept = sympy.solve(x_intercept_equacion, x)[0]
print(f"Intersección con el eje X:")
display(x_intercept)
Resultado:
Intersección con el eje X:
\(
-6
\)
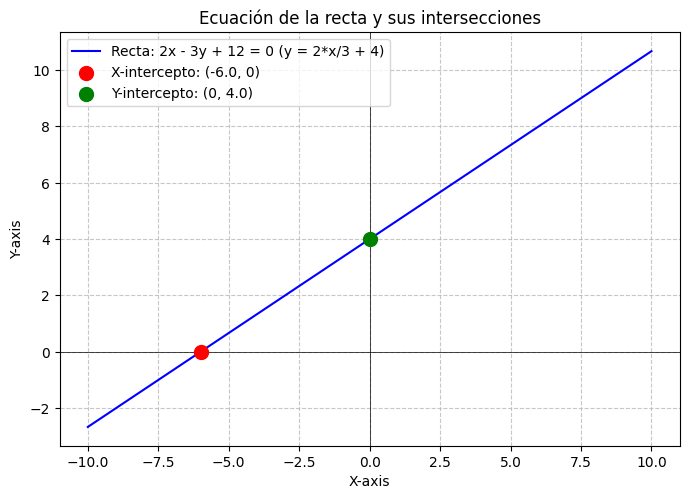
Graficamos la recta y sus intersecciones
Usarémos matplotlib para graficar la recya y sus intersecciones con los ejes. En esta oportunidad, usarémos también la librería Numpy para generar valores numéricos, y usarlos como parámetros en el módulo plot de Matplotlib.
# Convertimos las expresiones simbólicas de sympy en expresiones numéricas de numpy usando lambdify
y_func = sympy.lambdify(x, y_solved, 'numpy')
# Generamos valores de "x" para la recta
x_values = np.linspace(-10, 10, 400)
y_values = y_func(x_values)
plt.figure(figsize=(8, 6))
plt.plot(x_values, y_values, label=f'Recta: 2x - 3y + 12 = 0 (y = {y_solved})', color='blue')
# Graficamos las intersecciones con los ejes
plt.scatter(float(x_intercept), 0, color='red', s=100, zorder=5, label=f'X-intercepto: ({float(x_intercept)}, 0)')
plt.scatter(0, float(y_intercept), color='green', s=100, zorder=5, label=f'Y-intercepto: (0, {float(y_intercept)})')
plt.title('Ecuación de la recta y sus intersecciones')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.gca().set_aspect('equal', adjustable='box') # Asegurate que las escalas sean iguales
plt.show()
Resultado: