Mostrarémos que esta ecuación corresponde a una parábola usando sympy
import sympy as sym
# Definimos las variables
x, y = sym.symbols('x y')
# Definimos la expresión
expresion = 3*x**2 - 12*x + 4*y + 8
# Mostramos la expresión original
print("Expresión original:")
expresion
Resultado:
Expresión original:
\(
3x^2−12x+4y+8
\)
Si bién, no hay forma directa de factorizar la ecuación para darle forma de ecuación canónica de parábola, podemos jugar un poco con la función factor para lograrla
# Factorizamos los terminos de "x" y de "y" de forma separada
x_terminos = 3*x**2 - 12*x
y_terminos = 4*y + 8
factored_x_terms = sym.factor(x_terminos)
factored_y_terms = sym.factor(y_terminos)
# Combinamos las partes factorizadas
factored_expression_parts = factored_x_terms + factored_y_terms
print("Expresión Original:")
display(expresion)
print("Términos de 'x' factorizados:")
display(factored_x_terms)
print("Términos de 'y' factorizados:")
display(factored_y_terms)
print("Términos factorizados de 'x' e 'y' combinados:")
display(factored_expression_parts)
Resultado:
Expresión Original:
\(
3x^2 −12x + 4y + 8
\)
Términos de ‘x’ factorizados:
\(
3x(x−4)
\)
Términos de ‘y’ factorizados:
\(
4(y+2)
\)
Términos factorizados de ‘x’ e ‘y’ combinados:
\(
x(x−4)+4(y+2)
\)
Utilizarémos el módulo plot_implicit de sympy para graficar esta ecuación, de manera sencilla
from sympy.plotting import plot_implicit
# Renderizamos la expresión original igualándola a 0
plot_implicit
Resultado:
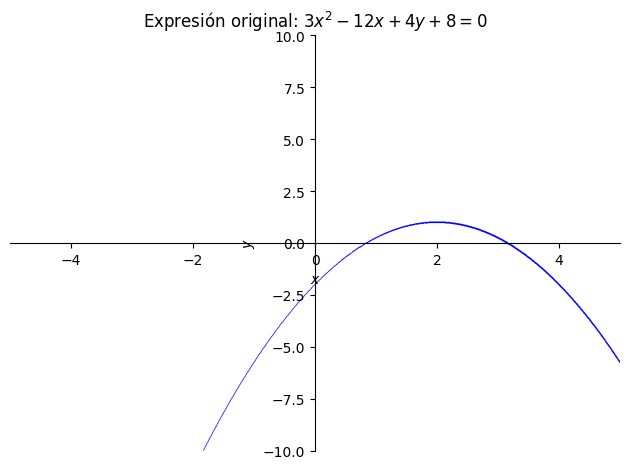
Ahora, alternativamente, generamos la gráfica usando Matplotlib. Es evidente que esta librería, pese a ser más compleja, nos da un mejor control de la gráfica a generar
import matplotlib.pyplot as plt
import numpy as np
# Definimos el rango de "x" dándole valores numéricos con Numpy
x_values = np.linspace(-2, 6, 400) # Choose a suitable range for x
# Calculamos los valores de "y" en la ecuación 3x^2 - 12x + 4y + 8 = 0
# Resolvemos, en función de "y": 4y = -3x^2 + 12x - 8
# y = (-3x^2 + 12x - 8) / 4
y_values = (-3 * x_values**2 + 12 * x_values - 8) / 4
# Generamos la gráfica
plt.figure(figsize=(8, 6))
#renderizamos la expresion en formato raw string (r'') para poder mostrar la expresión en formato LaTeX en la etiqueta
plt.plot(x_values, y_values, label=r'$3x^2 - 12x + 4y + 8 = 0$')
# Agregamos etiquetas y título
plt.xlabel('x')
plt.ylabel('y')
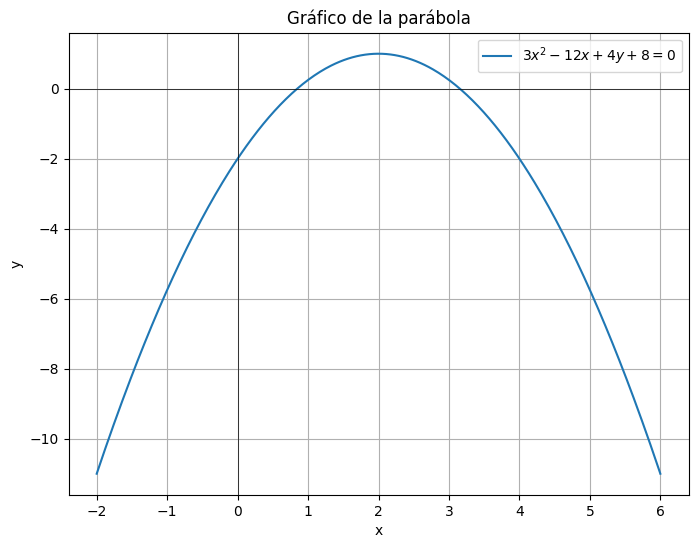
plt.title('Gráfico de la parábola')
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5) # Add x-axis
plt.axvline(0, color='black',linewidth=0.5) # Add y-axis
plt.legend()
plt.show()
Resultado: