Problemas de Razonamiento Matemático
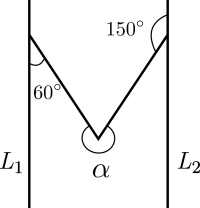
Si \(L_1\) y \(L_2\) son dos rectas paralelas, entonces ¿cuanto mide el ángulo \(\alpha\)?
\(300^{\circ}\)
\(270^{\circ}\)
\(210^{\circ}\)
\(90^{\circ}\)
\(110^{\circ}\)

\(300^{\circ}\)
\(270^{\circ}\)
\(210^{\circ}\)
\(90^{\circ}\)
\(110^{\circ}\)
En efecto, tracemos la recta \(L\) que es paralela a \(L_1\) y \(L_2\), y que pasa por el vértice del ángulo \(\alpha\).

Tenemos que:
\[ \alpha = \beta + \theta \hspace{3em} \boldsymbol{(1)} \]Como \(\beta\) es conjugado interno con el ángulo de \(60^{\circ}\), por la lección «ángulos», éstos son suplementarios. Luego:
\[ \beta + 60^{\circ} = 180^{\circ} \Rightarrow \beta = 120^{\circ} \hspace{2em} \boldsymbol{(2)} \]Como \(\theta\) es alterno interno con el ángulo de \(150^{\circ}\), por la lección «ángulos», éstos son congruentes. Luego:
\[ \theta = 150^{\circ} \hspace{4em} \boldsymbol{(3)} \]Luego, reemplazando (2) y (3) en (1):
\[ \alpha = 120^{\circ} + 150^{\circ} = \boldsymbol{270^{\circ}} \]Hipotenusa 2025
“Dame un punto de apoyo y moveré el mundo”
Arquímedes