Cal. Diferencial Sec. 4.6

Problemas de optimización

1. (Area Máxima). Hallar las dimensiones de un rectángulo de \(72 \, m\). de perímetro que encierra un área máxima.

2. (Area Máxima). Probar que entre todos los rectángulos de perímetro fijo, el que encierra un área máxima es el cuadrado.

3. (Area Máxima). Se quiere cercar un terreno rectangular que está a las orillas de un río. Si se cercan sólo tres lados del terreno y se cuenta con \(400 \, m\). de alambrada. ¿Qué dimensiones debe tener el terreno si se quiere que tenga área máxima?.

4. (Construcción de envases). Se construye cajas sin tapa utilizando láminas de cartón cuadrado de \(96 \, cm\). de lado, a las cuales se recorta un pequeño cuadrado en cada esquina. ¿Cuál debe ser la longitud del lado del cuadrado cortado si se quiere que la caja tenga volumen máximo?.

5. (Construcción de envases). Se construyen cajas sin tapa utilizando láminas de cartón rectangulares de \(21 \, cm\). por \(16 \, cm\)., a las cuales se recorta un pequeño cuadrado en cada esquina. ¿Cuál debe ser la longitud del lado del cuadrado si se quiere que la caja tenga máximo volumen?.

6. (Construcción de envases). Se construyen cajas con tapa utilizando láminas de cartón rectangulares de \(8 \, dm\). por \(5 \, dm\), a las cuales se les recortan los cuadrados y los rectángulos marcados en la figura adjunta.

   ¿Cuál debe ser la longitud del lado del cuadrado si se quiere que la caja tenga máximo volumen?.

   

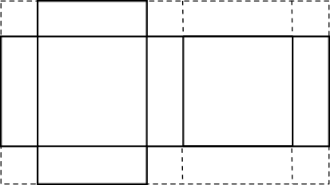
   ¿Cuál debe ser la longitud del lado del cuadrado si se quiere que la caja tenga máximo volumen?.

7. (Construcción de envases). Se construyen cajas con tapa, las cuales también tienen caras laterales.

   Para esto, se usan láminas de cartón rectangulares de \(9\, dm\). por \(6 \, dm\)., a las cuales se les recorta los 6 cuadrados indicados en la figura.

   

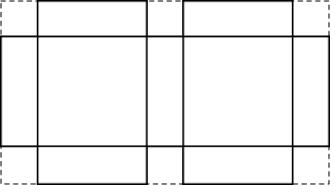
   Para esto, se usan láminas de cartón rectangulares de \(9\, dm\). por \(6 \, dm\)., a las cuales se les recorta los 6 cuadrados indicados en la figura.

   ¿Cuál debe ser la longitud del lado del cuadrado si se quiere que la caja tenga máximo volumen?.

8. (Volumen máximo). El reglamento del correo exige que la suma de las longitudes (largo, ancho y altura) de un paquete no debe exceder \(120 \, cm\).

   Hallar las dimensiones de la caja con base cuadrada, que cumpla las regulaciones del correo y que tenga máximo volumen.

   

   Hallar las dimensiones de la caja con base cuadrada, que cumpla las regulaciones del correo y que tenga máximo volumen.

9. (Pista de carreras). Se desea construir una pista de carreras de \(560 \, m\). de longitud. La pista debe encerrar un terreno que tenga la forma de un rectángulo con un semicírculo adjunto a cada uno de los lados opuestos del rectángulo.

   El rectángulo debe tener área máxima.

   Hallar las dimensiones del rectángulo.

   

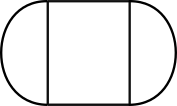
   El rectángulo debe tener área máxima.

   Hallar las dimensiones del rectángulo.

10. (Pista de carreras). Se desea construir una pista de carreras de \(400 \, m\). de longitud. La pista debe encerrar un terreno que tenga la forma de un rectángulo con un semicírculo adjunto a dos de los lados opuestos del rectángulo. ¿Cuál es la máxima área que puede tener el terreno encerrado?.

11. (Máxima claridad). Se desea construir una ventana con perímetro de \(7\, m.\) y que tenga la forma de un rectángulo coronado por un semicírculo.

    ¿Qué dimensiones debe tener si se quiere que ella deje pasar la máxima claridad?.

    Sugerencia: A mayor área, mayor claridad.

    

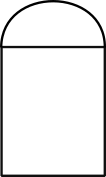
    ¿Qué dimensiones debe tener si se quiere que ella deje pasar la máxima claridad?.

    Sugerencia: A mayor área, mayor claridad.

12. (Máxima claridad). Una ventana de 18 pies de perímetro está conformada por un rectángulo coronado por un triángulo equilátero.

    El vidrio que cubre el rectángulo es más claro que el que cubre el triángulo. Por pie cuadrado, el vidrio del rectángulo deja pasar el doble de luz del que cubre el triángulo.

    Hallar las dimensiones de la ventana que dejan pasar la máxima claridad.

    

    El vidrio que cubre el rectángulo es más claro que el que cubre el triángulo. Por pie cuadrado, el vidrio del rectángulo deja pasar el doble de luz del que cubre el triángulo.

    Hallar las dimensiones de la ventana que dejan pasar la máxima claridad.

13. (Costo mínimo). Dos puntos \(A\)   y   \(B\) están opuestos uno al otro en las riberas de un río de \(3 \, Km\). de ancho.

    Un tercer punto \(C\) está en la misma ribera que \(B\) pero a \(7 \, Km\). río abajo. Una compañía telefónica desea unir telefónicamente los puntos \(A\) y \(C\). Para esto, se debe tender dos cables: Uno de \(A\) a un punto \(P\), en la ribera opuesta, y el otro cable de \(P\) a \(C\).

    

    Un tercer punto \(C\) está en la misma ribera que \(B\) pero a \(7 \, Km\). río abajo. Una compañía telefónica desea unir telefónicamente los puntos \(A\) y \(C\). Para esto, se debe tender dos cables: Uno de \(A\) a un punto \(P\), en la ribera opuesta, y el otro cable de \(P\) a \(C\).

    Si el tendido del cable en el agua cuesta \(\$ 17,000\) el \(Km\). y en tierra cuesta \(\$ 8,000\) el \(Km\)., ¿dónde debe estar localizado el punto \(P\) para que el costo sea mínimo?.

14. (Costo mínimo). En el problema anterior, si el tendido de cable en el agua cuesta \(\$ 13,000\) el \(Km\). y en tierra \(\$ 12,000\), ¿dónde debe estar localizado el punto \(P\)?.

15. (Tiempo mínimo). Una isla se encuentra a \(4.8\, Km\). de una playa recta.

    En la playa, a \(6 \, Km\). del punto \(F\) que está frente la isla, funciona una tienda.

    Un hombre que está en la isla quiere ir a la tienda. Se sabe que el hombre rema a \(3 \, Km./h\). y camina a \(5 \, Km./h\).

    

    En la playa, a \(6 \, Km\). del punto \(F\) que está frente la isla, funciona una tienda.

    Un hombre que está en la isla quiere ir a la tienda. Se sabe que el hombre rema a \(3 \, Km./h\). y camina a \(5 \, Km./h\).

    ¿Qué camino debe seguir para llegar a la tienda en el menor tiempo posible?.

16. (Tiempo mínimo). Si en el problema anterior el hombre rema a razón de \(4 \, Km./h\) y camina a razón de \(5 \, Km./h\). ¿Qué camino debe seguir?.

17. (Hotelería). Un hotel tiene 100 habitaciones. El gerente sabe que cuando el precio por habitación es de \(\$ 45\) todas las habitaciones son rentadas; pero por cada dólar de aumento, una habitación se desocupa.

    Si el precio de mantenimiento de una habitación ocupada es de \(\$ 5\), ¿cuántas habitaciones deben rentarse para obtener máxima ganancia?. ¿Cuál debe ser el precio por habitación?.

18. (Agricultura). Una granja está sembrada de mangos a razón de 80 plantas por hectárea. Cada planta produce un promedio de 960 mangos. Por cada planta adicional que se siembre, el promedio de producción por planta se reduce en 10 mangos.

    ¿Cuántas plantas se deben sembrar por hectárea para obtener la máxima producción?.

19. (Area Máxima).

    Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un semicírculo de radio \(r\).

    

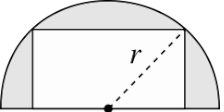
    Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un semicírculo de radio \(r\).

20. (Volumen máximo). Se planea construir un canal de concreto para transportar agua a una granja.

    La sección transversal del canal es como se indica en la figura, teniendo la base y las paredes laterales una misma longitud \(b\).

    

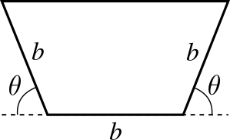
    La sección transversal del canal es como se indica en la figura, teniendo la base y las paredes laterales una misma longitud \(b\).

    Hallar el ángulo \(\theta\) que permite que el canal transporte el mayor volumen de agua.

    Sugerencia: Exprese el área del trapecio en términos de \(\theta\) y maximice.

21. (Area Máxima). Hallar las dimensiones del rectángulo de área máxima, de lados paralelos a los ejes y que puede inscribirse en la región acotada por las parábolas:

    \[ y = 4 - \frac{x^2}{3}, \quad y = \frac{x^2}{6} - 2 \]
    \[ y = 4 - \frac{x^2}{3}, \quad y = \frac{x^2}{6} - 2 \]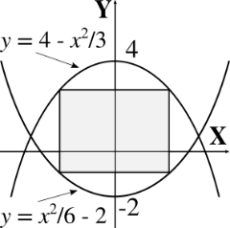

    

22. (Resistencia Máxima). De un tronco circular de radio \(3 \, dm\). se quiere cortar una viga rectangular de máxima resistencia. Hallar las dimensiones del rectángulo. Se sabe que la resistencia de una viga rectangular es directamente proporcional a su ancho y al cuadrado de su altura. Es decir, \(R = kah^2\), donde \(R\) es la resistencia, \(k\) es una constante de proporcionalidad, \(a\) es el ancho del rectángulo y \(h\) su altura.

23. (Area Mínima). Un trozo de alambre de \(12 \, m\). se corta en dos partes. Una parte se doblará para formar una circunferencia y la otra se doblará para formar un cuadrado.

    ¿Dónde se hará el corte?, si:

    1. La suma de las áreas es mínima.

    2. La suma de las áreas es máxima.

    

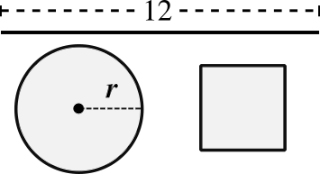
    ¿Dónde se hará el corte?, si:

    1. La suma de las áreas es mínima.

    2. La suma de las áreas es máxima.

24. (Area Máxima).

    Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo equilátero de \(12 \, cm\). de lado, de tal modo que un lado del rectángulo descanse sobre un lado del triángulo.

    Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo equilátero de \(12 \, cm\). de lado, de tal modo que un lado del rectángulo descanse sobre un lado del triángulo.

    

25. (Area Máxima). Probar que de todos los triángulos isósceles de perímetro fijo, el que tiene área máxima es un triángulo equilátero.

26. (Area Máxima). Probar que de todos los triángulos isósceles inscritos en una circunferencia, el que tiene área máxima es un triángulo equilátero.

27. (Area Máxima).

    Se inscribe un trapecio en un semicírculo de radio 2, en tal forma que un lado del trapecio coincide con el diámetro.

    Se inscribe un trapecio en un semicírculo de radio 2, en tal forma que un lado del trapecio coincide con el diámetro.

    

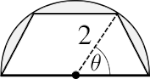
    Hallar máxima posible área del trapecio.

28. (Area lateral máxima). Hallar las dimensiones del cilindro circular recto de área lateral máxima inscrito en una esfera de radio \(r\).

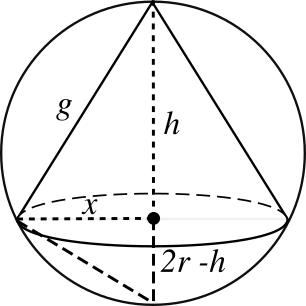
29. (Volumen máximo). Hallar las dimensiones del cono circular recto de volumen máximo inscrito en una esfera de radio \(r\).

    Sugerencia:   \(V = \text{Volumen del cono} = \frac{1}{3} \pi x^2 h\)

    Por semejanza de triángulos:   \(x^2 = h(2r - h)\)

    Luego:   \(V = \frac{ 1}{3} \pi h^2 (2r - h)\)

    

    Sugerencia:   \(V = \text{Volumen del cono} = \frac{1}{3} \pi x^2 h\)

    Por semejanza de triángulos:   \(x^2 = h(2r - h)\)

    Luego:   \(V = \frac{ 1}{3} \pi h^2 (2r - h)\)

30. (Area lateral máxima). Hallar las dimensiones del cono circular recto de área lateral máxima inscrito en una esfera de radio \(r\).

    Ver la figura del problema anterior.

    Sugerencia:   \(A = \text{Area lateral del cono} = \pi x g\).

31. (Volumen máximo).

    Probar que el volumen del mayor cilindro circular recto inscrito en un cono circular recto es \(\frac{4}{9}\) del volumen del cono.

    Probar que el volumen del mayor cilindro circular recto inscrito en un cono circular recto es \(\frac{4}{9}\) del volumen del cono.

    

32. (Area máxima). Se construye una figura conformada por un triángulo isósceles de \(10 \, cm\). de lado al que se le adjunta un semicírculo, como indica el dibujo adjunto.

    Hallar:

    1. El ángulo \(\theta\) correspondiente a la figura de área máxima.

    2. El área máxima.

    

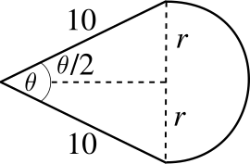
    Hallar:

    1. El ángulo \(\theta\) correspondiente a la figura de área máxima.

    2. El área máxima.

    Sugerencia: Ver el problema resuelto 1.1.5.

33. (Cerco mínimo). Se quiere construir una pequeña granja rectangular de \(7.200 \, m^2\) de área a la orilla de un río.

    Si sólo se requiere cercar los tres lados (como indica la figura), ¿que longitudes deben tener estos lados si quiere invertir la menor cantidad posible de cerco?.

    

    Si sólo se requiere cercar los tres lados (como indica la figura), ¿que longitudes deben tener estos lados si quiere invertir la menor cantidad posible de cerco?.

34. (Cerco mínimo). Se quiere cerrar un terreno rectangular y luego dividirlo en dos partes iguales mediante una cerca como indica la figura.

    El área de terreno encerrado debe ser de \(864 \, m^2\).

    El área de terreno encerrado debe ser de \(864 \, m^2\).

    

    Si se desea utilizar la mínima cantidad de cerca, ¿qué dimensiones debe tener el rectángulo?.

35. (Area mínima). Se quiere construir una caja cerrada de madera de \(72 \, dm^3\) de volumen. La base debe ser un rectángulo cuyo largo sea el doble de su ancho.

    1. ¿Qué dimensiones debe tener la caja si se quiere que la cantidad de madera de la cual estarà compuesta la caja sea mínima?.

    2. ¿Qué dimensiones debe tener la caja si no tiene tapa?.

36. (Area mínima). Se quiere imprimir un libro, en el cual cada página tenga como márgenes: \(3 \, cm\). superior e inferior y \(2 \, cm\) de cada lado.

    El texto escrito debe ocupar un área de \(294 \, cm^2\).

    Si se busca economizar papel, ¿qué dimensiones de la página son las más convenientes?.

    

    El texto escrito debe ocupar un área de \(294 \, cm^2\).

    Si se busca economizar papel, ¿qué dimensiones de la página son las más convenientes?.

37. (Area máxima). Se tiene un terreno rectangular de \(480 \, m^2\). de área, sobre el cual se va a construir una casa que tendrá también forma rectangular. Para jardines se dejaran \(5 \, m\) de frente, \(5\, m\). atrás y \(4 \, m\). a los costados. ¿Qué dimensiones debe tener el terreno para que el área de la casa sea máxima?.

38. (Area mínima). Para envasar sus productos una compañía necesita envases cilíndricos de hojalata de \(2\pi \; dm^3\) de capacidad y con tapa. Si se busca usar la mínima cantidad de hojalata, ¿qué dimensiones debe tener cada envase?.

39. (Area mínima). Resolver el problema anterior para el caso en que el envase no tenga tapa superior.

40. (Volumen máximo). Se quiere construir vasos (cilíndricos sin tapa) de vidrio que tengan \(108 \pi \, cm^2\). de material. ¿Qué dimensiones debe tener el vaso si se quiere que contenga la mayor cantidad de líquido?.

41. (Velocidad más económica). Un bus debe hacer un viaje de \(500 \, Km\). a una velocidad constante \(x \, Km./h\). La gasolina cuesta \(\$ 0.5\) por litro, el bus consume \(2 + \frac{x^2}{200}\) litros por hora, y el conductor cobra \(\$ 15\) por hora. ¿Cuál es la velocidad más económica?.

42. (Ley de reflexión).

    Usando el principio de Fermat (la luz viaja de un punto a otro a través de la trayectoria que minimiza el tiempo) probar que:

    Si la luz parte de \(A\) se refleja en un espejo y pasa por el punto \(B\), entonces el ángulo de incidencia \(i\) es igual al ángulo de reflexión \(r\).

    

    Usando el principio de Fermat (la luz viaja de un punto a otro a través de la trayectoria que minimiza el tiempo) probar que:

    Si la luz parte de \(A\) se refleja en un espejo y pasa por el punto \(B\), entonces el ángulo de incidencia \(i\) es igual al ángulo de reflexión \(r\).

43. (Areas optimas). Se tiene una hoja larga de papel de \(24 \, cm\). de ancho.

    Una esquina de es doblada en tal forma que el vértice doblado toque el lado opuesto, como se indica en la figura.

    Una esquina de es doblada en tal forma que el vértice doblado toque el lado opuesto, como se indica en la figura.

    

    Hallar el valor de \(x\) para el cual:

    1. El triángulo \(A\) tenga área máxima.

    2. El triángulo \(B\) tenga área mínima.

44. (Volumen mínimo).

    Hallar las dimensiones de un cono circular recto de volumen mínimo que se puede circunscribir en un hemisferio (semiesfera) de radio \(8 \, cm\).

    Hallar las dimensiones de un cono circular recto de volumen mínimo que se puede circunscribir en un hemisferio (semiesfera) de radio \(8 \, cm\).

    

45. (Longitud mínima). Frente a un edificio, y a 27 pies de distancia, se tiene una pared de 8 pies de altura.

    Hallar la longitud de la escalera más corta que pueda apoyarse en el suelo, la pared y el edificio.

    

    Hallar la longitud de la escalera más corta que pueda apoyarse en el suelo, la pared y el edificio.

46. (Altura mínima).

    Hallar la altura mínima \(h = \overline{OP}\) que debe tener una puerta de una torre para que a través de ella pueda pasar un tubo \(\overline{AB}\) de longitud \(6\sqrt{6} \, m\).

    Hallar la altura mínima \(h = \overline{OP}\) que debe tener una puerta de una torre para que a través de ella pueda pasar un tubo \(\overline{AB}\) de longitud \(6\sqrt{6} \, m\).

    El ancho de la torre es \(2\sqrt{2} \, m\).

    

    El ancho de la torre es \(2\sqrt{2} \, m\).