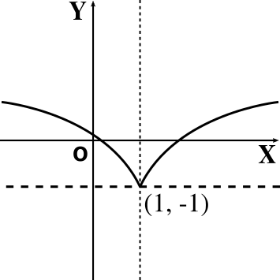1. Eje Y
2. Origen
3. Eje X, eje Y y Origen
4. Eje X, eje Y y Origen
5. Eje X
6. Eje X
7. Eje X, eje Y y Origen
8. \((x – 2)^2 + (y + 1)^2 = 25\)
9. \((x + 3)^2 + (y – 2)^2 = 5\)
10. \(x^2 + y^2 = 25\)
11. \((x – 1)^2 + (y + 1)^2 = 50\)
12. \((x – 1)^2 + (y + 3)^2 = 9\)
13. \((x + 4)^2 + (y – 1)^2 = 16\)
14. \((x – 3)^2 + (y – 1)^2 = 10\)
15. \((x – 1)^2 + y^2 = 1\)
16. \((x – 3)^2 + (y – 4)^2 = 25\)
17. Centro \((1, \, 0), \; r= 2\)
18. Centro \((0, \, -2), \; r = 2 \sqrt{2}\)
19. Centro \(\left( 0, \, -\frac{1}{2} \right), \; r = \frac{1}{2} \)
20. Centro \((1, \, -2), \; r = 3 \)
21. Centro \(\left( \frac{1}{4}, \, -\frac{1}{4} \right), \; r = \frac {\sqrt{10}}{4}\)
22. Centro \(\left( \frac{3}{2}, \, \frac{1}{2} \right), \; r = \frac{9}{4}\)
23. \[ (y – 1)^2 = (x + 1)^3 \]

    

24. \[ (x – 1)^2 = (y + 1)^3 \]

    

25. \[ (y + 1)^2 = (x – 1)^3 \]

    

26. \[ (x-3)^2 (y – 2) = 4 \left(2 -(y – 2) \right) \]

    

27. \[ (y – 3)^2 (x – 2)= 4 \left( 2 – (x-2) \right) \]

    

28. \[ (x + 3)^2 (y + 2) = 4 \left( 2 -(y + 2) \right) \]

    

En los problemas del 1 al 7, aplicar los criterios de simetría para determinar si el gráfico de la ecuación dada es simétrico respecto al eje X, eje Y o al origen.

1. \[ y = x^2 \]
2. \[ xy = 1 \]
3. \[ \frac{x^2}{4} + \frac{y^2}{9} = 1 \]
4. \[ \frac{x^2}{4} – \frac{y^2}{9} = 1 \]
5. \[ y^2(2 – x) = x^3 \]
6. \[ x^2 + y^2 + x = \sqrt{x^2+y^2} \]
7. \[ (x^2 + y^2)^2 = x^2 – y^2 \]

En los problemas del 8 al 16, hallar una ecuación de la circunferencia que satisface las condiciones dadas.

8. Centro, \((2, -1)\);   \(r = 5\).
9. Centro \((-3, 2)\);   \(r =\sqrt{5}\).
10. Centro en el origen, pasa por \((-3, 4)\).
11. Centro \((1, -1)\), pasa por \((6, 4)\).
12. Centro \((1, -3)\), es tangente al eje X.
13. Centro \((-4, 1)\), es tangente al eje Y.
14. Tiene un diámetro de extremos: \((2, 4)\)   y   \((4, -2)\).
15. Radio \(r = 1\) pasa por: \((1, 1)\)   y   \((1, -1)\).
16. Pasa por los puntos \((0, 0)\), \((0, 8)\)   y   \((6, 0)\).

En los problemas del 17 al 22, probar que la ecuación dada representa una circunferencia, hallando su centro y su radio.

17. \[ x^2 + y^2 – 2x – 3 = 0 \]
18. \[ x^2 + y^2 + 4y – 4 = 0 \]
19. \[ x^2 + y^2 + y = 0 \]
20. \[ x^2 + y^2 – 2x + 4y – 4 = 0 \]
21. \[ 2x^2 + 2y^2 – x + y – 1 = 0 \]
22. \[ 16x^2 + 16y^2 – 48x – 16y – 41 = 0 \]

En los problemas 23, 24 y 25, aplicando los criterios de traslación a la gráfica de la parábola semicúbica (ejemplo 2.2.6-b), graficar las siguientes ecuaciones.

23. \[ (y – 1)^2 = (x + 1)^3 \]
24. \[ (x – 1)^2 = (y + 1)^3 \]
25. \[ (y+1)^2 = (x – 1)^3 \]

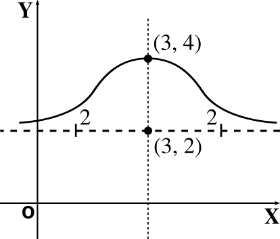
En los problemas del 26 al 28, aplicando los criterios de traslación y de reflexión a la gráfica de la Bruja de Agnesi (ejemplo 2.2.6-a), graficar las siguientes ecuaciones.

26. \[ (x-3)^2(y-2)=4(4-y) \]
27. \[ (y – 3)^2(x – 2) = 4(4 – x) \]
28. \[ (x + 3)^2(y + 2) = 4(-y) \]