2. \[ y = 5x – 2 \]
3. \[ y = -3x \]
    
4. \[ y = 2x – 1 \]
    
5. \[ y = – \frac{2}{5}x + 2 \]
    
6. \[ y = – \frac{3}{5} x + \frac{18}{5} \]
    
7. \[ y = \frac{x}{5}+ \frac{11}{5} \]
    
8. \[ y = -2x + \frac{41}{23} \]
    
9. \[ x + y = 2;\,x – y = 14 \]
    
10.  
    1. \[ y = – \frac{x}{2} + \frac{3}{2} \]
        
    2. \[ \frac{ 9 \sqrt{5}}{10} \]
        
11. \[ 5 \]
     
12. \(L_2\) es paralela a \(L_5\);   \(L_3\) es perpendicular a \(L_1\);   \(L_4\) es perpendicular a \(L_6\).
13.  
    1. \[ x – 3y – 6 = 0 \]
        
    2. \[ x + 2y – 13 = 0 \]
        
    3. \[ y = 1 \]
        
14. \[ y + 3x – 25 = 0 \]
     
15. \[ 3 \]
     
16. \[ 2 \]
     
17. \[ \frac{2}{\sqrt{10}} \]
     
18. \[ 2 \]
     
19. \[ \frac{ 4 \sqrt{10} }{5} \]
     
20. \[ \frac{28}{5} \]
     
21. \[ C = -7 \; \text{ ó } \; C = \frac{59}{3} \]
     
22. \(5x + 12y + 40 = 0\);   \(5x + 12y – 64 = 0\)
23. \[ 3x – 4y + 7 = 0 \]
     
24. \(5x – 3y – 34 = 0\);   \(3x + 5y + 34 = 0\)
25. \[ (5, \, -3) \; \text{ y } \; (-3, \, -5) \]
     
26. \[ x – y – 3 \sqrt{2} = 0; \; x – y + 3 \sqrt{2} = 0 \]
    \[ \begin{aligned} &x – y – 3 \sqrt{2} = 0; \\[.5em] &x – y + 3 \sqrt{2} = 0 \end{aligned} \]
27. \[ 3x + 4y – 14 = 0 \]
     
28. \[ (x – 1)^2 + (y + 1)^2 = 9 \]
     
29. \[ x^2 + y^2 = 16 \]
     
30. \[ (x – 2)^2 + (y – 4)^2 = 10 \]
     
31. \[ (x + 2)^2 + (y + 1)^2 = 20 \]
     
32. \[ 3x – 2y – 12 = 0; \, 3x – 8y + 24 = 0 \]
     
33.  
    1. \[ k \neq 3, \, n \text{ cualquiera} \]
        
    2. \[ k = -\frac{4}{3}, \, n \text{ cualquiera} \]
        
    3. \[ k = 3, \, n \neq 6 \]
        
    4. \[ k = 3, \, n = 6 \]
        
34.  
    1. \(k = -4\)   y   \(n \neq 2\)   ó   \(k = 4\)   y   \(n \neq -2\)
    2. \(k = -4\)   y   \(n = 2\)   ó   \(k = 4\)   y   \(n = -2\)
    3. \(k = 0\)   y   \(n\) cualquiera
35. \(x – 2y – 18 = 0\);   \(2x + y + 14 = 0\);   \(2x + y – 16 = 0\)

38. \(A = \left( 0, \, \frac{14}{5} \right)\),   \(B = \left( \frac{7}{4}, \, 0\right)\)

1. Usando pendientes probar que los puntos \(A = (2, 1)\), \(B = (-4, -2)\),   y   \(C = (1, 1/2)\) son colineales.

En los problemas del 2 al 9, hallar una ecuación de la recta que satisface las condiciones dadas y llevarla a la forma} \(\boldsymbol{y = mx + b}\).

2. Pasa por el punto (1, 3) y tiene pendiente 5.
3. Tiene pendiente -3 y pasa por el origen.
4. Pasa por los puntos \((1, 1)\) y \((2, 3)\).
5. Interseca al eje X en 5 y al eje Y en 2.
6. Pasa por el punto \((1, 3)\) y es paralela a la recta \(5y + 3x – 6 = 0\).
7. Pasa por el punto \((4, 3)\)   y es perpendicular a la recta \(5x + y – 2 = 0\).
8. Es paralela a \(2y + 4x – 5 = 0\) y pasa por el punto de intersección de las rectas:
   \[ 5x + y = 4 \text{,} \quad 2x + 5y – 3 = 0 \]
9. Interseca a los ejes coordenados a igual distancia del origen y pasa por \((8, -6)\).
10. Dada la recta \(L:\, 2y – 4x – 7 = 0\):
    1. Encontrar la recta que pasa por el punto \(P = (1, 1)\) y es perpendicular a \(L\).
    2. Hallar la distancia del punto \(P = (1, 1)\) a la recta \(L\).
11. Usando pendientes probar que los puntos \(A = (3, 1)\), \(B = (6, 0)\)   y   \(C = (4, 4)\) son los vértices de un triángulo rectángulo. Hallar el área de dicho triángulo.
12. Determinar cuáles de las siguientes rectas son paralelas y cuáles son perpendiculares:
    1. \[ L_1:\, 2x + 5y – 6 = 0 \]
    2. \[ L_2: \, 4x + 3y – 6 = 0 \]
    3. \[ L_3: \, -5x + 2y – 8 = 0 \]
    4. \[ L_4: \, 5x + y – 3 = 0 \]
    5. \[ L_5: \, 4x + 3y – 9 = 0 \]
    6. \[ L_6: \, -x + 5y – 20 = 0 \]
13. Hallar la mediatriz de cada uno de los siguientes segmentos de extremos:
    27. \[ (1, \, 0) \, \text{ y } \, (2, \, -3) \]
    28. \[ (-1, \, 2) \, \text{ y } \, (3, \, 10) \]
    29. \[ (-2, \, 3) \, \text{ y } \,(-2, \, -1) \]
14. Los extremos de una de las diagonales de un rombo son \((2, -1)\) y \((14, 3)\). Hallar una ecuación de la recta que contiene a la otra diagonal.

    Sugerencia: las diagonales de un rombo son perpendiculares.

15. Hallar la distancia del origen a la recta \(4x + 3y -15 = 0\).
16. Hallar la distancia del punto \((0, -3)\) a la recta \(5x – 12y – 10 = 0\).
17. Hallar la distancia del punto \((1, -2)\) a la recta \(x – 3y = 5\).
18. Hallar la distancia entre las rectas paralelas \(3x – 4y = 0\), \(3x – 4y = 10\).
19. Hallar la distancia entre las rectas paralelas \(3x – y + 1 = 0\), \(3x – y + 9 = 0\).
20. Hallar la distancia de \(Q = (6, -3)\) a la recta que pasa por \(P = (-4, 1)\) y es paralela a la recta \(4x + 3y = 0\).
21. Determinar el valor de \(C\) en la recta \(L: \, 4x +3y + C = 0\) sabiendo que la distancia del punto \(Q = (5, 9)\) a \(L\) es 4 veces la distancia del punto \(P = (-3, 3)\) a \(L\).
22. Hallar las rectas paralelas a la recta \(5x + 12y – 12 = 0\) y que distan 4 unidades de ésta.
23. Hallar la ecuación de la recta que es tangente en el punto \((-1, 1)\) a la circunferencia \(x^2 + y^2 – 4x + 6y – 12 = 0\).
24. Hallar las ecuaciones de las dos rectas que pasan por el punto \(P = (2, -8)\) y son tangentes a la circunferencia \(x^2 + y^2 = 34\).
25. En el problema anterior, hallar los puntos de contacto de las tangentes con la circunferencia.
26. Hallar las ecuaciones de las dos rectas paralelas a la recta \(2x – 2y + 5 = 0\) y que son tangentes a la circunferencia \(x^2 + y^2 = 9\).
27. Hallar la ecuación de la recta que es tangente en el punto \((2, 2)\) a la circunferencia \(x^2 + y^2 + 2x + 4y – 20 = 0\).
28. Hallar la ecuación de la circunferencia de centro \(C = (1, -1)\) que es tangente a la recta \(5x – 12y + 22 = 0\).
29. Hallar la ecuación de la circunferencia que pasa por \(Q = (4, 0)\) y es tangente a la recta \(3x – 4y + 20 = 0\) en el punto \(P = (-12/5, \,16/5)\).
30. Hallar la ecuación de la circunferencia que pasa por los puntos \((3, 1)\) y \((-1, 3)\) y su centro está en la recta \(3x – y – 2 = 0\).
31. Hallar la ecuación de la circunferencia que es tangente a las rectas paralelas: \(2x + y -5 = 0\), \(2x + y +15 = 0\). \(B = (2, 1)\) es uno de los puntos de tangencia.
32. Hallar la ecuación de la recta que pasando por el punto \(P = (8, 6)\) intersecta a los ejes coordenados formando un triángulo de área 12 unidades cuadradas.
33. Determinar para que valores de \(k\) y de \(n\) las rectas:
    \[ kx – 2y – 3 = 0 \text{,} \quad 6x – 4y – n = 0 \]
    \[ \begin{aligned} &kx – 2y – 3 = 0 \text{,} \\[1em] &6x – 4y – n = 0 \end{aligned} \]
    1. Se intersecan en un único punto.
    2. Son perpendiculares.
    3. Son paralelas no coincidentes.
    4. Son coincidentes.
34. Determinar para que valores de \(k\) y de \(n\) las rectas:
    \[ kx + 8y + n = 0 \text{,} \quad 2x + ky – 1 = 0 \]
    \[ \begin{aligned} &kx + 8y + n = 0 \text{,} \\[1em] &2x + ky – 1 = 0 \end{aligned} \]
    1. Son paralelas no coincidentes.
    2. Son coincidentes.
    3. Son perpendiculares.
35. Un cuadrado tiene por centro \(C = (1, -1)\) y uno de sus lados está en la recta \(x-2y = -12\). Hallar las ecuaciones de las rectas que contienen a los otros lados.
36. Probar que los puntos \(A = (1, 4)\), \(B = (5, 1)\), \(C = (8, 5)\)   y   \(D = (4, 8)\) son los vértices de un rombo (cuadrilátero de lados de igual longitud). Verifique que las diagonales se cortan perpendicularmente.
37. Sean \(a\) y \(b\) la abscisa en el origen y la ordenada en el origen de una recta.

    Si \(a \neq 0\)   y   \(b \neq 0\), probar que una ecuación de esta recta es   \( \frac{x}{a} + \frac{y}{b} = 1 \).

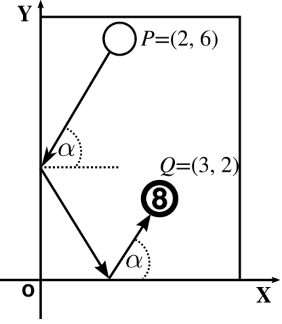
38. Roberto está defiendo los colores de su club en un campeonato de billar.

    En determinado momento, él debe golpear la bola ocho con una bola blanca, ejecutando un tiro sin efecto, y usando 2 bandas (como indica la figura).

    Si la bola blanca está en el punto \(P = (2, 6)\) y la bola ocho en \(Q = (3, 2)\), hallar los puntos, \(A\) y \(B\), en los extremos de la mesa donde la bola debe impactar para ganar la jugada.

    

    Si la bola blanca está en el punto \(P = (2, 6)\) y la bola ocho en \(Q = (3, 2)\), hallar los puntos \(A\)   y   \(B\) en los extremos de la mesa donde la bola debe tocar para que la jugada tenga éxito.