1. \[ \frac{x^2}{36} + \frac{y^2}{32} = 1 \]
    
2. \[ \frac{x^2}{39} + \frac{y^2}{64} = 1 \]
    
3. \[ \frac{(x – 4)^2}{4} + \frac{(y – 2)^2}{3} = 1 \]
    
4. \[ \frac{(x + 4)^2}{16} + \frac{(y – 3)^2}{25} = 1 \]
    
5. \[ (x – 3)^2 + \frac{( y – 1 )^2 }{4} = 1 \]
    
6. \[ \frac{ x^2 }{25} + \frac{y^2}{9} = 1 \]
    
7. \[ \frac{ (x + 1)^2 }{4} + \frac{y^2}{9} = 1 \]
    
8. \[ \frac{ (x – 2)^2 }{ \frac{1600}{91} } + \frac{y^2}{100} = 1 \]
    
9. \[ \frac{ x^2 }{9} + \frac{y^2}{5} = 1 \]
    
10. \[ \frac{(x + 1)^2}{8} + \frac{(y + 4)^2}{9} = 1 \]
     
11. \[ \frac{x^2}{36} + \frac{(y + 1)^2}{27} = 1 \]
     
12. \[ \frac{(x + 2)^2}{25} + \frac{(y – 2)^2}{10} = 1 \]
     
13.  
    1. \(\cfrac{(x – 3)^2}{4} + \cfrac{(y + 2)^2}{1} = 1\)
    2. Vértices: \((1, \, -2)\),   \((5, \, -2)\).   Focos: \(\left( 3 – \sqrt{3}, \, -2 \right)\),   \(\left( 3 + \sqrt{3}, \, -2 \right)\)
14.  
     
    1. \(\cfrac{ (x – 1)^2 }{4} + \cfrac{(y + 3)^2}{9} = 1\)
    2. Vértices: \((1, \, -6)\),   \((1, \, 0)\).   Focos: \(\left( 1, \, -3 -\sqrt{5} \right)\),   \(\left(1, \, -3 + \sqrt{5} \right)\)
15.  
    1. \(\cfrac{(x + 2)^2}{16} + \cfrac{(y – 3)^2}{25} = 1\)
    2. Vértices: \((-2, \, -2)\),   \((-2, \, 8)\).   Focos: \((-2, \, 0)\),   \((-2, \, 6)\)
16. Sí. La altura del tunel cuando \(x = 9\) es \(8\), y \(7.5 < 8\).
17. \[ \frac{ x^2 }{(240)^2} + \frac{y^2}{(140)^2} = 1 \]
     
18. \[ \frac{x^2}{16} + \frac{y^2}{12} = 1. \; \text{ Elipse}. \]
     
19. \[ \frac{x^2}{9} + \frac{y^2}{25} = 1. \; \text{ Elipse}. \]
     
20.  
    1. \[ e = \frac{8}{17} \]
    2. \[ \frac{x^2}{ 18,062,500 } + \frac{ y^2 }{ 14,062,500 } = 1 \]
       \[ \begin{aligned} \frac{x^2}{ 18,062,500 } &+ \frac{ y^2 }{ 14,062,500 } \\[.5em] &\hspace{3em} = 1 \end{aligned} \]

En los problemas del 1 al 12, hallar la ecuación canónica de la elipse con los datos son indicados.

1. Focos: \((\pm 2, 0)\). Vértices: \((\pm 6, 0)\).
2. Focos: \((0, \pm 5)\). Vértices: \((0, \pm 8)\)
3. Foco: \((5, 2)\). Vértices: \((2, 2)\), \((6, 2)\).
4. Foco: \((-4, 0)\). Vértices: \((-4, -2)\), \((-4, 8)\).
5. Vértices: \((3, -1)\), \((3, 3)\). Pasa por \((2, 1)\).
6. Vértices: \((\pm 5, 0)\), Longitud del eje menor: 6.
7. Vértices: \((-1, \pm 3)\). Longitud del eje menor: 4.
8. Vértices: \((2, -10)\), \((2, 10)\). Pasa por \((6, 3)\).
9. Focos: \((\pm 2, 0)\). Excentricidad : \(e=2/3\).
10. Vértices: \((1, 1)\), \((1, 7)\). Excentricidad: \(e=1/3\).
11. Focos: \((\pm 3, -1)\). Longitud lado recto = 9.
12. Centro: \((-2, 2)\). Vértice: \((3, 2)\). Lado recto = 4.
13. \[ x^2 + 4y^2 – 6x + 16y = – 9 \]
14. \[ 9x^2 + 4y^2 -18x + 24y + 9 = 0 \]
15. \[ 25x^2 + 16y^2 +100x – 96y = 156 \]

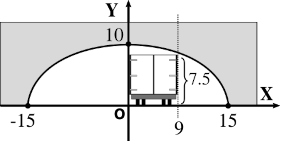
16. Una autopista de dos vías pasa por un túnel semi-elíptico de 10 pies de altura y 30 pies de ancho.

    Un camión de 9 pies de ancho y 7.5 pies de altura se acerca al túnel por su lado de la autopista.

    

    ¿Podrá el camion atravesar el túnel sin rozar el puente, ni usar la otra línea de la autopista?

17. La sección trazada a lo largo de la parte más larga del Estadio Olímpico de Montreal es una elipse con eje mayor y eje menor de 480 y 280 metros, respectivamente. Hallar la ecuación canónica de esta elipse.

    Este estadio fue construido con motivo de las olimpiadas del año 1976. La torre inclinada que se observa mide 175 metros, y es la más alta de su tipo.

    

    Este estadio fue construido con motivo de las olimpiadas del año 1976. La torre inclinada que se observa mide 175 metros, y es la más alta de su tipo.

18. Sea \(S\) el conjunto de puntos \(P\) del plano, tales que la distancia de \(P\) al punto (2, 0) es la mitad de la distancia de \(P\) a la recta \(x = 8\). Hallar una ecuación que satisfaga los puntos de \(S\). Identificar este conjunto.
19. Sea \(S\) el conjunto de puntos \(P\) del plano, tales que la distancia de \(P\) al punto (0, 4) es 4/5 de la distancia \(P\) a la recta \(y = \frac{25}{4}\). Hallar una ecuación que satisfaga los puntos de \(S\).
20. Se ha colocado un satélite que gira alrededor de la luna. Su órbita es una elipse, y el centro lunar coincide con uno de sus focos. Las distancias, máxima y mínima, a la superficie lunar son 4,522 y 522 kilómetros, respectivamente. Si el radio de la luna es 1,728 kilómetros, hallar:
    1. la excentricidad de la órbita.
    2. una ecuación de la órbita.

21. Sea la elipse:   \(\cfrac{x^2}{a^2}+ \cfrac{y^2}{b^2}=1\);   y sea \(P = (x_1, \, y_1)\) un punto de ella.

    1. Probar que la pendiente de la tangente a la elipse en el punto \(P=(x_1, \, y_1)\) es:

       \[ m = -\frac{b^2x_1}{a^2y_1} \]

       Sugerencia: La recta \(T: \, y = m(x -x_1) + y_1\)   pasa por   \(P = (x_1, \, y_1)\). T es tangente a la elipse si intersecta a ésta en un único punto. Seguir los mismos pasos del problema resuelto 3.2.6.

       Otra sugerencia: Espera hasta que aprendas a derivar.

    2. Probar que la recta tangente \(T\) a la elipse en el punto \(P = (x_1, \, y_1)\), tiene por ecuación:   \(\cfrac{x_1 x}{a^2} + \cfrac{y_1 y}{b^2}=1\).