1.  
   1. \(y = x^3 – 3\)

      

   2. \(y = (x – 1)^3\)

      

   3. \(y = -x^3 + 1\)

      

   4. \(-y = (x – 1)^3 + 1\)

      

2.  
   1. \(y = \cfrac{1}{x} – 2\)

      

   2. \(y = \cfrac{1}{x-2}\)

      

   3. \(y = – \cfrac{1}{x}\)

      

   4. \(y = \cfrac{1}{x – 2} + 5\)

      

3.  
   1. \(y = – \lfloor x \rfloor\)

      

   2. \(y = \lfloor 2x \rfloor\)

      

   3. \(y = \cfrac{1}{2} \lfloor x \rfloor \)

      

4.  

   1. 

5.  

   1. 

   2. periodo \(= \cfrac{2 \pi}{4} = \cfrac{\pi}{2}\)
6. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = (-\infty, \, 1) \cup (1, \, 2]\), \(\text{Dom}\left( \frac{f}{g} \right) = ( – \infty, \, 1 ) \cup (1, \, 2 )\)
7. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = [-4, \, -2] \cup [2, \, 4],\) \(\text{Dom}\left( \frac{f}{g} \right) = [-4, \, -2)\) \(\cup (2, \, 4]\)
8. \(\text{Dom}(f + g) = \text{Dom}(f – g)\) \(= \text{Dom}(fg) = (-2, \, 2)\), \(\text{Dom}\left( \frac{f}{g} \right) = (-2, \, 2) – \{ 0 \}\)
9. \(\text{Dom}(f) = 4\)
10. \(\text{Dom}(f) = (-2, \, 0]\)
11. \(\text{Dom}(g) = [-2, \, 3 )\)
12. \((f \circ g)(x) = x – 1\),   \(\text{Dom}(f \circ g) = [0, \, +\infty)\) \((g \circ f)(x) = \sqrt{ x^2 – 1 }\),   \(\text{Dom}(g \circ f) = (-\infty, \, -1] \cup [1, \, +\infty)\) \((f \circ f)(x) = x^4 – 2x^2\),   \(\text{Dom}(f \circ f) = \mathbb{R}\) \((g \circ g)(x) = \sqrt[4]{x}\),   \(\text{Dom}(g \circ g) = [0, \, +\infty)\)
13. \((f \circ g)(x) = x – 4\),   \(\text{Dom}(f \circ g) = [4, \, +\infty)\), \((g \circ f)(x) = \sqrt{ x^2 – 4 }\),   \(\text{Dom}(g \circ f) = (-\infty, \, -2] \cup [2, \, +\infty)\) \((f \circ f)(x) = x^4\),   \(\text{Dom}(f \circ f) = \mathbb{R}\) \((g \circ g)(x) = \sqrt{ \sqrt{x – 4} – 4 }\),   \(\text{Dom}(g \circ g) = [20, \, +\infty)\)
14. \((f \circ g)(x) = \cfrac{1}{x^2} – \cfrac{1}{x}\),   \(\text{Dom}(f \circ g) = \mathbb{R}- \{ 0 \}\) \((g \circ f)(x) = \cfrac{1}{x^2 – x}\),   \(\text{Dom}(g \circ f) = \mathbb{R} – \{ 0, \, 1 \}\) \((f \circ f)(x) = x^4 – 2x^3 + x\),   \(\text{Dom}(f \circ f) = \mathbb{R}\) \((g \circ g)(x) = x\),   \(\text{Dom}(g \circ g) = \mathbb{R} – \{ 0 \}\)
15. \((f \circ g)(x) = \cfrac{ 1 }{1 – \sqrt[3]{x}}\),   \(\text{Dom}(f \circ g) = \mathbb{R} – \{ 1 \}\) \((g \circ f)(x) = \cfrac{1}{\sqrt[3]{ 1 – x }}\),   \(\text{Dom}(g \circ f) = \mathbb{R} – \{ 1 \}\) \((f \circ f)(x) = \cfrac{x – 1}{x}\),   \(\text{Dom}(f \circ f) = \mathbb{R} – \{ 0, \, 1\}\) \((g \circ g)(x) = \sqrt[9]{x}\),   \(\text{Dom}(g \circ g) = \mathbb{R}\)
16. \((f \circ g)(x) = \sqrt{-x}\),   \(\text{Dom}(f \circ g) =(-\infty, \, 0]\) \((g \circ f)(x) = \sqrt{ 1 – \sqrt{ x^2 – 1 } }\),   \(\text{Dom}(g \circ f) = \left[ -\sqrt{2}, \, -1 \right]\) \(\cup \left[ 1, \, \sqrt{2} \right] \) \((f \circ f)(x) = \sqrt{x^2 – 2}\),   \(\text{Dom}(f \circ f) = \left( -\infty, \, -\sqrt{2} \right]\) \(\cup \left[ \sqrt{2}, \, +\infty \right)\) \((g \circ g)(x) = \sqrt{ 1 – \sqrt{ 1 – x } }\),   \(\text{Dom}(g \circ g) = [0, \, 1]\)
17. \[ (f \circ g \circ h)(x) = \sqrt{ \frac{1}{x^2 – 1} } \]
     
18. \[ (f \circ g \circ h)(x) = \sqrt[3]{ \frac{x^2 – x}{ x^2 – x + 1 } } \]
     
19. \((f \circ f \circ f)(x) = x, \)   \(\text{Dom}(f \circ f \circ f) = \mathbb{R}- \{ 0, \, 1 \}\)
20. \[ f(x) = \frac{1}{x}, \, g(x) = 1 + x \]
     
21. \[ f(x) = x-3, \, g(x) = \sqrt{x} \]
     
22. \[ f(x) = \sqrt[3]{x}, \, g(x) = (2x – 1)^2 \]
     
23. \[ f(x) = \frac{1}{x}, \, g(x) = \sqrt{ x^2 – x + 1 } \]
     
24. \(f(x) = \cfrac{1}{x + 1}\),   \(g(x) = \cfrac{1}{x}\),   \(h(x) = x^2\)
25. \(f(x) = \sqrt[3]{x}\),   \(g(x) = x + 1\),   \(h(x) = x^2 + \mid x \mid\)
26. \(f(x) = \sqrt[4]{x}\),   \(g(x) = x – 1\),   \(h(x) = \sqrt{x}\)
27. \[ g(x) = x^2 – 2x + 1 \]
     
28. \[ g(x) = \frac{1}{x + 1} \]
     

1. Usando la gráfica de   \(f(x)=x^3\), bosquejar los gráficos de:

   1. \[ y = x^3 – 3 \]
   2. \[ y = (x -1)^3 \]
   3. \[ y = -x^3 + 1 \]
   4. \[ y = -(x-1)^3 + 1 \]

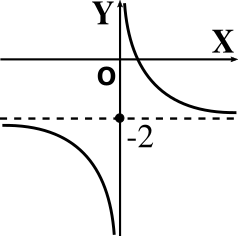
2. Usando la gráfica de   \(f(x)=\cfrac{1}{x}\), bosquejar los gráficos de:

   1. \[ y = \frac{1}{x} -2 \]
   2. \[ y = \frac{1}{x-2} \]
   3. \[ y = – \frac{1}{x} \]
   4. \[ y = \frac{1}{x-2} +5 \]

3. Usando la gráfica de \( y = \lfloor x \rfloor \), bosquejar el gráfico de:

   1. \[ y = – \lfloor x \rfloor \]
   2. \[ y = \lfloor 2x \rfloor \]
   3. \[ y = \frac{1}{2} \lfloor x \rfloor \]

4. Utilizando la gráfica de la función   \(y=\text{sen} x\)   y las técnicas de traslación y reflexión, graficar la función   \(y=1- \text{sen}(x – \frac{\pi}{2})\)

5. Considerando la gráfica   \(y= \cos x\):

   1. Usando las técnicas de la transformación de gráficas, bosquejar la gráfica de   \( y = -3\cos 4x\).

   2. ¿Cuál es el periodo de   \(y = -3\cos 4x\)?

En los problemas 6, 7 y 8 hallar \(\boldsymbol{f+g,\; f-g,\; fg}\)   y   \(\boldsymbol{f/g}\) con sus dominios.

6. \[ f(x) = \cfrac{1}{1-x},\quad g(x) = \sqrt{2-x} \]
7. \[ f(x) = \sqrt{16-x^2},\quad g(x) = \sqrt{x^2-4} \]
   \[ \begin{aligned} &f(x) = \sqrt{16-x^2}, \\[1em] &g(x) = \sqrt{x^2-4} \end{aligned} \]
8. \[ f(x) = \cfrac{1}{\sqrt{4-x^2}},\quad g(x) = \sqrt[3]{x} \]

En los problemas 9, 10 y 11 hallar el dominio de la función dada.

9. \[ f(x) = \sqrt{4-x} + \sqrt{x-4} \]
10. \[ f(x) = \sqrt{-x} + \cfrac{1}{\sqrt{x+2}} \]
11. \[ g(x) = \cfrac{ \sqrt{3-x} + \sqrt{x+2} }{ x^2-9 } \]

En los problemas del 12 al 16 hallar   \(\boldsymbol{f \circ g,\,g \circ f,\,f \circ f}\)   y   \(\boldsymbol{g \circ g}\), con sus respectivos dominios.

12. \[ f(x) = x^2-1,\; g(x) = \sqrt{x} \]
13. \[ f(x) = x^2,\; g(x) = \sqrt{x-4} \]
14. \[ f(x) = x^2-x,\; g(x) = \cfrac{1}{x} \]
15. \[ f(x) = \cfrac{1}{1-x},\; g(x) = \sqrt[3]{x} \]
16. \[ f(x) = \sqrt{x^2-1},\; g(x) = \sqrt{1-x} \]

En los problemas 17 y 18 hallar   \(\boldsymbol{f \circ g \circ h}\).

17. \(f(x) = \sqrt{x}\),   \(g(x) = \cfrac{1}{x}\),   \(h(x) = x^2-1\)

18. \(f(x) = \sqrt[3]{x}\),   \(g(x) = \cfrac{x}{1+x}\),   \(h(x) = x^2-x\)

19. Si   \(f(x)=\cfrac{1}{1-x}\), hallar, con su respectivo dominio, \(f \circ f \circ f\).

En los problemas del 20 al 23 hallar dos funciones \(\boldsymbol{f}\)   y   \(\boldsymbol{g}\)   tales que   \(\boldsymbol{F=f \circ g}\).

20. \[ F(x) = \cfrac{1}{1+x} \]
21. \[ F(x) = -3 + \sqrt{x} \]
22. \[ F(x) = \sqrt[3]{ (2x-1)^2 } \]
23. \[ F(x) = \cfrac{1}{ \sqrt{ x^2 – x + 1 } } \]

En los problemas 24, 25 y 26 hallar   \(\boldsymbol{f,\, g}\)   y   \(\boldsymbol{h}\) tales que:

24. \[ F(x) = \frac{x^2}{1+x^2} \]
25. \[ F(x) = \sqrt[3]{ x^2 + \mid x \mid + 1 } \]
26. \[ F(x) = \sqrt[4]{ \sqrt{x} – 1 } \]
27. Si   \(f(x)=2x+3\)   y   \(h(x)=2x^2-4x+5\),   hallar una función   \(g\)   tal que   \(f \circ g=h\).
28. Si   \(f(x)=x-3\)   y   \(h(x)=\cfrac{1}{x-2}\),   hallar una función   \(g\)   tal que   \(g \circ f= h\).