Problema 109
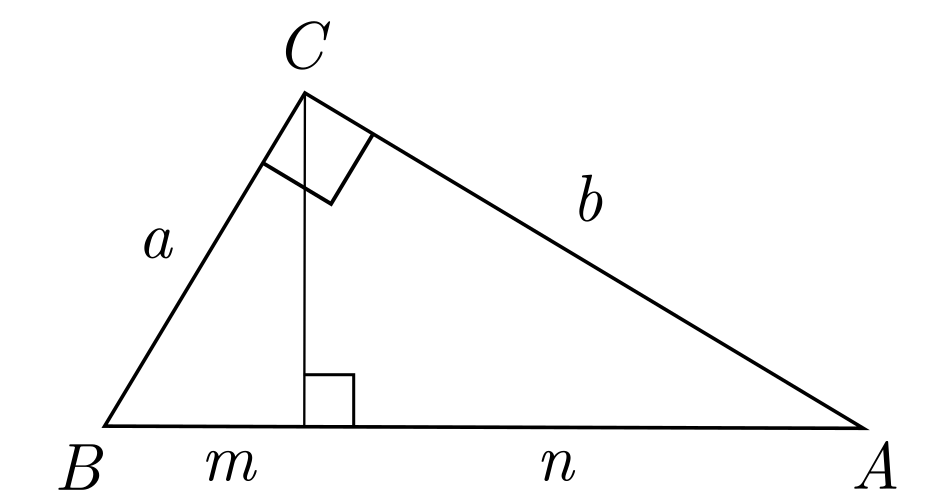
Del triángulo \( \triangle ABC \) de la figura adjunta, se sabe que \( \frac{a}{b} = \frac{1}{3} \), entonces \( \frac{n}{m} \) es:
-
\( \frac{1}{ \sqrt{3} } \)
-
\( 3 \)
-
\( \frac{1}{3} \)
-
\(9\)
-
\( \frac{1}{9} \)
Intenta resolverlo antes de ver la respuesta...
Los lados del ángulo \( \angle \alpha \) son perpendiculares a los lados del ángulo \( \angle \beta \). Por la lección Propiedades el Triangulo, estos son congruentes:
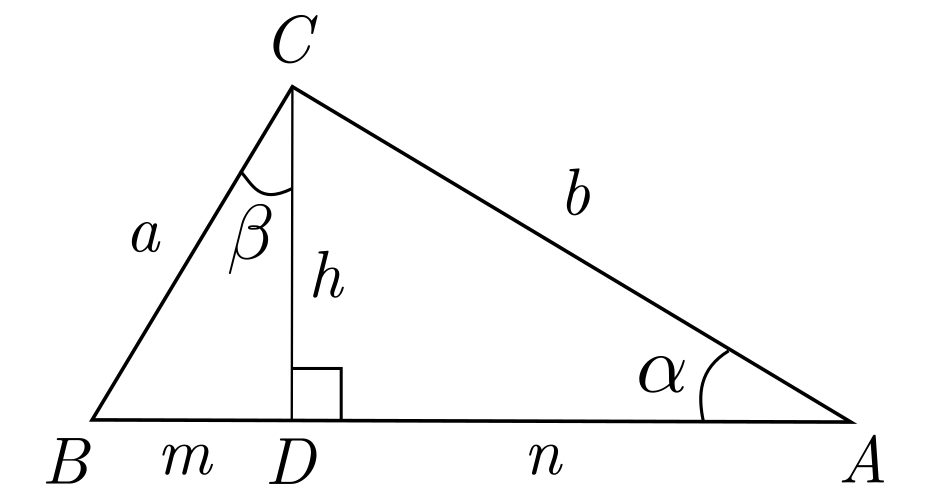
En consecuencia, por la lección Propiedades del Triangulo, los triángulos \( \triangle ACB \) y \( \triangle CDB \) son semejantes. Por lo tanto:
\[ \frac{a}{b} = \frac{m}{h} \]Pero, \( \cfrac{a}{b} = \cfrac{1}{3} \).
Luego, \( \cfrac{m}{h} = \cfrac{1}{3} \)
Entonces:
\[ \boldsymbol{(1)} \hspace{2em} m = \frac{h}{3} \]Por las mismas razones, los triángulos rectángulos \( \triangle CDB \) \( \triangle CDA \) son semejantes. Por lo tanto:
\[ \frac{a}{h} = \frac{b}{n} \Rightarrow an = bh \]Entonces:
\[ \boldsymbol{(2)} \hspace{2em} n = \frac{b}{a} (h) \]Pero,
\[ \frac{a}{b} = \frac{1}{3} \Rightarrow \frac{b}{a} =3 \]Luego, reemplazando en \( (2) \) tenemos:
\[ \boldsymbol{(3)} \hspace{2em} n = 3h \]Finalmente, de \((1)\) y \((3)\) obtenemos:
\[ \begin{aligned} \frac{n}{m} &= \frac{3h}{ \frac{h}{3} } \\[2em] &= \frac{9h}{h} = \boldsymbol{9} \end{aligned} \]
