Precálculo Sec. 3.2

La parábola

En los problemas del 1 al 5, hallar el foco, la directriz y longitud \(\boldsymbol{L}\) del lado recto de la parábola indicada.

1. \[ x^2=4y \]
2. \[ 3x^2 + 4y= 0 \]
3. \[ y^2 - 6x = 0 \]
4. \[ y^2 + 20x = 0 \]
5. \[ 4y^2 + x = 0 \]

En los problemas del 6 al 10, hallar el vértice, el eje, el foco, la directriz y la longitud \(\boldsymbol{L}\) del lado recto de la parábola indicada.

6. \[ x^2-4x-8y=-12 \]
7. \[ y^2+10y=x-26 \]
8. \[ y^2-4y=2x+4 \]
9. \[ 4x^2+4x+4y+1=0 \]
10. \[ 9x^2+24x+72y+88=0 \]

En los problemas del 11 al 23, hallar la ecuación de la parábola que tiene las propiedades indicadas.

11. Foco \((-6, 0)\), directriz: \(x = 6\)
12. Foco \((0, 4)\), directriz: \(y = -4\)
13. Foco \((2, 5)\), directriz: \(y=-1\)
14. Foco \(\left( -\frac{7}{8}, -2 \right)\), directriz: \(x = - \frac{9}{8}\)
15. Vértice \((-2, 2)\), directriz: \(x = 2\)
16. Vértice \((-2, 2)\), directriz: \(y=-2\)
17. Vértice \((3, 1)\), foco: \((3, 5)\)
18. Vértice \((0, 0)\), eje: \(x = 0\), pasa por \((3, -2)\)
19. Vértice (1, 2), eje: paralelo al eje X, pasa por (5, 8)
20. Vértice \((1,-2)\), eje: paralelo al eje Y, longitud lado recto: 6
21. Directriz: \(x=-2\), eje: \(y=1\), longitud lado recto: 8
22. Puntos extremos del lado recto: \((1, 1)\)   y   \((7, 1)\). Se abre hacia arriba.
23. Vértice \((0, 0)\), extremos del lado recto: \((-4, \, k)\)   y   \((4, \, k)\). Se abre hacia abajo.

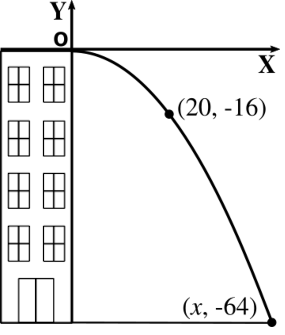
24. Una pelota es lanzada horizontalmente desde la orilla de una azotea de un edificio de 64 \(m\) de altura.

    La trayectoria de la pelota es una parábola cuyo vértice está en la orilla del edificio y su eje está a lo largo del muro. La pelota pasa por un punto que está a 20 \(m\) del muro cuando la distancia vertical es de 16 \(m\).

    1. Hallar una ecuación de la trayectoria, ubicando el origen de coordenadas en el vértice y el eje Y coincide con el eje de la parábola.
    2. Hallar la distancia al muro del punto donde la pelota golpea el suelo.

    

    1. Hallar una ecuación de la trayectoria, ubicando el origen de coordenadas en el vértice y el eje Y coincide con el eje de la parábola.
    2. Hallar la distancia al muro del punto donde la pelota golpea el suelo.
25. Un faro está construido por un espejo parabólico de 12 \(cm\). de diámetro y un radio de 2 \(cm\). de profundidad. ¿A qué distancia del vértice se debe colocarse la fuente luz para que los rayos se reflejen paralelamente al eje de la parábola?
26. La orilla de una antena parabólica es una circunferencia de 1 \(m\) de diámetro y en su centro está el receptor de los rayos que vienen del exterior. Hallar la profundidad de la antena.
27. Las torres de un puente colgante están a 150 \(m\) de distancia y tiene una altura de 23 \(m\). El cable entre las torres tiene forma parabólica y su punto más bajo está a 8 \(m\) sobre la carretera.
    1. Hallar una ecuación de la parábola generada por el cable.
    2. Hallar la altura que está el cable en el punto de la vía que está a 15 \(m\). del pie de la torre.

28. Un puente se sostiene sobre un arco parabólico de concreto.

    El arco tiene una abertura de 200 pies al nivel del agua y una altura en su centro de 50 pies.

    1. Hallar una ecuación de la parábola introduciendo un sistema de coordenadas como indica la figura.
    2. Hallar la altura del arco sobre el nivel del agua en el punto que está a 70 pies del extremo derecho del arco.

    

    1. Hallar una ecuación de la parábola introduciendo un sistema de coordenadas como indica la figura.
    2. Hallar la altura del arco sobre el nivel del agua en el punto que está a 70 pies del extremo derecho del arco.
29. La órbita de un cometa es una parábola en cuyo foco está el sol. Cuando el cometa está 60 millones de \(Km\). del sol, la recta que pasa por el sol y el cometa forma un ángulo de \(60^{\circ}\) con el eje de la parábola. Hallar la mínima distancia del cometa al sol.

30. Se colocó un satélite de órbita parabólica con foco en el centro de la luna.

    Cuando el satélite está a 5,814 \(km\). de la superficie lunar, el eje de la parábola y la recta que pasa por el satélite y el centro de la luna forman un ángulo de \(60^{\circ}\). La distancia más corta del satélite a la superficie lunar es de 150 \(km\).

    Hallar el radio de la luna.

    Sugerencia:   \(p = 150 + r\),   y   problema resuelto 3.2.5

    

    Hallar el radio de la luna.

    Sugerencias:   \(p = 150 + r\),   y   problema resuelto 3.2.5

31. Hallar la ecuación canónica de la parábola cuyo eje es paralelo al eje X y pasa por los puntos \((3, 1)\), \((4, 3)\)   y   \((12, 7)\).

    Sugerencia: Los puntos satisfacen la ecuación} \((y- h)^2 = 4p(x- k)\).

32. Hallar la ecuación canónica de la parábola cuyo eje es paralelo al eje Y y pasa por los puntos \((1, 0)\), \((-1, 6)\)   y   \((2, 3)\).
33. Probar que la tangente a la parábola \(y^2 = 4px\) en cualquier punto \(P=(x_1, y_1)\) tiene por ecuación:   \(y_1y = 2p(x + x_1)\).

    Sugerencia: Problema resuelto 3.2.6.